Nos artigos anteriores, aprendemos um pouco sobre o Número de Euler, em
Limite Fundamental Exponencial pt. 1, e depois vimos como ele se relaciona com o Limite Fundamental Exponencial,
em
Limite Fundamental Exponencial pt. 2 .
Neste artigo você verá a resolução de exercícios sobre o limite fundamental
exponencial com acompanhamento gráfico.
a) $$\lim_{x \to -\infty} \left(1 - \frac{1}{x}\right)^{x}$$
b) $$\lim_{n \to 0} (1 + n)^{\frac{1}{n}}$$
c) $$\lim_{n \to -\infty} \left(1 + \frac{1}{n}\right)^{\frac{n}{2}}$$
d) $$\lim_{n \to -\infty} \left(1 + \frac{1}{n}\right)^{\frac{4}{3}n}$$
e) $$\lim_{n \to -\infty} \left(1 + \frac{1}{2n}\right)^{n}$$
Resolução
a) $$\lim_{x \to -\infty} \left(1 - \frac{1}{x}\right)^{x}$$
Primeiro passo: realizar a substituição de x
$$\frac{-1}{x} = \frac{1}{n}$$
$$-n = x$$ ou $$x = -n$$
Segundo passo: observar a tendência
- $$x = 10 \Rightarrow n = -10$$
- $$x = -10 \Rightarrow n = 10$$
- $$x = -100 \Rightarrow n = 100$$
- ...
- $$x \to -\infty \Rightarrow n \to +\infty$$
Quando x tende a menos infinito, n tendo a mais infinito.
Terceiro passo: montagem e resolução
$$\lim_{n \to +\infty} \left(1 + \frac{1}{n}\right)^{-n}$$ $$ = $$ $$\left(\lim_{n \to +\infty} \left(1 + \frac{1}{n}\right)^{n}\right)^{-1}$$ $$ = $$ $$e^{-1}$$ $$ = $$ $$\frac{1}{e}$$
Gráfico da função original
|
|
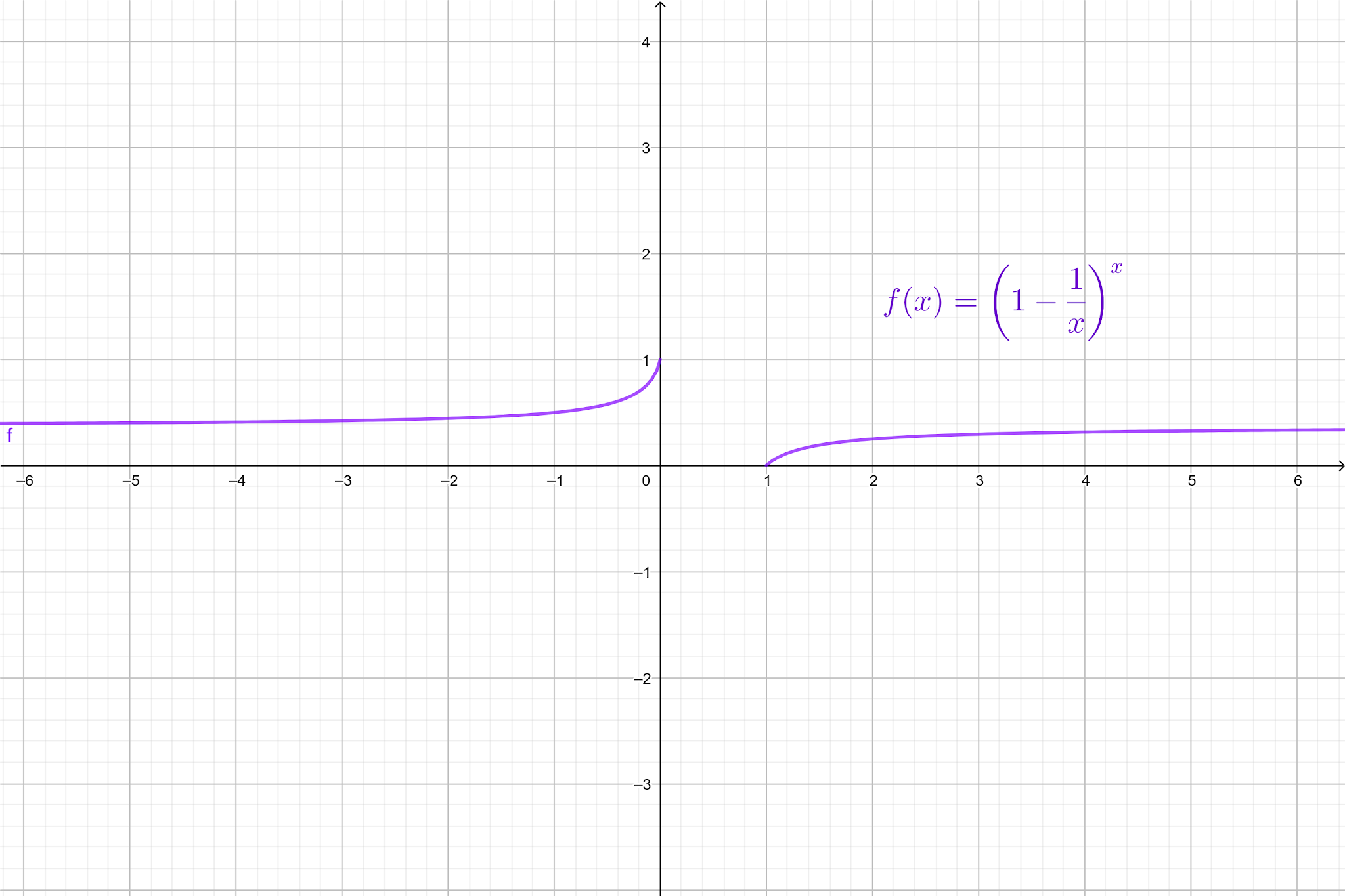
Gráfico da original função: quando x tende a
- infinito, f(x) se aproxima de
1/e |
Gráfico da segunda função
|
| Gráfico da função original: quando n tende a + infinito, g(n) se aproxima de 1/e |
b) $$\lim_{n \to 0} (1 + n)^{\frac{1}{n}} = e$$
Primeiro passo: realizar a substituição de n
$$n = \frac{1}{x}$$ $$\Rightarrow$$ $$x = \frac{1}{n}$$
Segundo passo: observar a tendência
- $$n = 1 \Rightarrow x = 1$$
- $$n = 0.1 \Rightarrow x = 10$$
- $$n = 0.01 \Rightarrow x = 100$$
- $$n = -1 \Rightarrow x = -1$$
- $$n = -0.1 \Rightarrow x = -10$$
- $$n = -0.01 \Rightarrow x = -100$$
- ...
- $$n \to 0 \Rightarrow x \to \pm\infty$$
Terceiro passo: montagem e resolução
$$\lim_{x \to +\infty} (1 + \frac{1}{x})^{x} = e$$
$$\lim_{x \to -\infty} (1 + \frac{1}{x})^{x} = e$$
Tabela
| n | g(n) |
|---|---|
| 1 | 2 |
| 0.1 | 2.5937424601 |
| 0.01 | 2.70481382942153 |
| 0.001 | 2.71692393223559 |
| -0.1 | 2.86797199079244 |
| -0.01 | 2.73199902642903 |
| -0.001 | 2.71964221644285 |
Gráfico
|
|
g(n) se aproxima de e quando n tende
a 0 |
c) $$\lim_{n \to -\infty} \left(1 + \frac{1}{n}\right)^{\frac{n}{2}}$$
$$ = $$ $$\lim_{n \to -\infty} \left(1 + \frac{1}{n}\right)^{\frac{1}{2}n}$$
$$ = $$ $$\left(\lim_{n \to -\infty} \left(1 +
\frac{1}{n}\right)^{n}\right)^{\frac{1}{2}}$$ $$ = $$ $$e^{\frac{1}{2}}$$ $$ =
$$ $$\sqrt{e}$$
Gráfico (considere x = n)
|
|
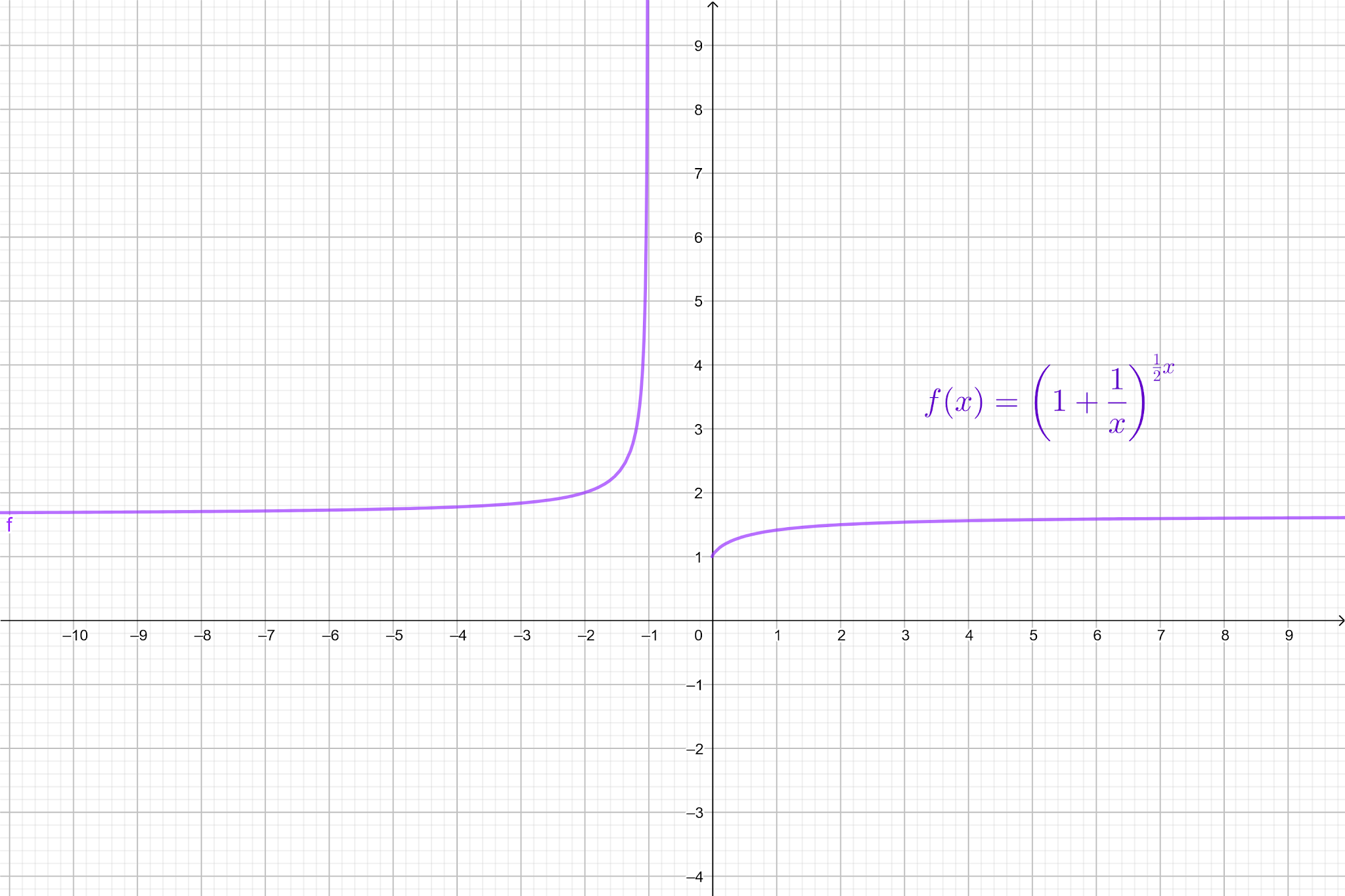
Quando f(x) se aproxima de -infinito, x se
aproxima da raiz quadrada de e. |
d) $$\lim_{n \to -\infty} \left(1 + \frac{1}{n}\right)^{\frac{4}{3}n}$$ $$ = $$ $$\left(\lim_{n \to -\infty} \left(1 + \frac{1}{n}\right)^{n}\right)^{\frac{4}{3}}$$ $$ = $$ $$e^{\frac{4}{3}}$$ $$ = $$ $$\sqrt[3]{e^{4}}$$
Gráfico (considere x = n)
|
| Quando f(x) se aproxima de -infinito, x se aproxima de ∛e⁴ |
e) $$\lim_{n \to -\infty} \left(1 + \frac{1}{2n}\right)^{n}$$
Primeiro passo: realizar a substituição de n
$$\frac{1}{2n} = \frac{1}{x}$$
$$x = 2n \Rightarrow n = \frac{x}{2}$$
Segundo passo: observar a tendência
- $$n = 10 \Rightarrow x = 20$$
- $$n = -10 \Rightarrow x = -20$$
- $$n = -100 \Rightarrow x = -200$$
- ...
- $$n \to -\infty \Rightarrow x \to -\infty$$
Terceiro passo: montagem e resolução
$$\lim_{x \to -\infty} \left(1 + \frac{1}{x}\right)^{\frac{x}{2}}$$ $$ = $$ $$\left(\lim_{x \to -\infty} \left(1 + \frac{1}{x}\right)^{x}\right)^{\frac{1}{2}}$$ $$ = $$ $$e^{\frac{1}{2}}$$ $$ = $$ $$\sqrt{e}$$
Gráfico
|
|
Quando a variável das funções tendem a - infinito, as
funções se aproximam da raiz quadrada de e. |
Note que para a resolução destes exercícios foi necessário aplicar as Propriedade dos Limites listadas neste artigo. No próximo artigo veremos sobre o Limite Fundamental Trigonométrico.
Para citar esse artigo:
muito bom. Obrigado!
ResponderExcluirQue isso, ficamos feliz que tenha gostado :)
Excluir