No artigo anterior, aprendemos sobre a continuidade de uma função com limites e como identificá-la. O tema a seguir é sobre mais um tipo de limite: o limite fundamental exponencial. Este tema foi dividido em duas partes: a primeira, uma breve introdução ao cálculo de juros com a explicação do número de Euler e, a segunda, a relação desses dois tópicos com os limites.
O Cálculo de Juros
Segundo o dicionário Priberam da Língua Portuguesa (2020), juro é um "rendimento de dinheiro emprestado". Existem duas modalidades para o cálculo desse rendimento, através de:
- Juros simples
- Juros compostos
Juros Simples
O juro simples é mais fácil de entender. Suponha o exemplo fictício em que seja feito um investimento de R$ 100,00 em um fundo imobiliário durante 4 meses. A cada mês, o rendimento do dinheiro é de 5% do capital investido. Então temos a seguinte situação:
- Capital (C): R$ 100,00
- Taxa (i): 5% a.m (ao mês)
- Tempo (t): 4 meses
| Mês | Rendimento do Mês | Montante |
|---|---|---|
| Jan | R$ 5,00 | R$ 105,00 |
| Fev | R$ 5,00 | R$ 110,00 |
| Mar | R$ 5,00 | R$ 115,00 |
| Abr | R$ 5,00 | R$ 120,00 |
A cada mês houve o rendimento de R$ 5,00 (5% de R$ 100,00) do capital do investido (R$ 100,00). Em 4 meses o investimento rendeu, no total, R$ 20,00 e o montante (M) da aplicação foi de R$ 120,00. A conta fica:
$$\text{J}_{\text{simples}} = C \cdot i \cdot t$$
$$J = 100 \cdot 0.05 \cdot 4 = 20 \text{ reais}$$
$$\text{M} = \text{C} + \text{J}$$
$$\text{M} = 100 + 20 = 120 \text{ reais}$$
Juros Compostos
Em Juros compostos ocorre o cálculo de "juros sobre juros" (ou rendimento sobre rendimento). Suponha um segundo exemplo fictício, em que foi aplicado R$ 100,00 durante 4 meses em um outro tipo de fundo imobiliário, ainda com a mesma taxa, ficando:
- Capital (C): R$ 100,00
- Taxa (i): 5% a.m (ao mês)
- Tempo (t): 4 meses
| Mês | Rendimento do Mês | Montante |
|---|---|---|
| Jan | R$ 5,00 | R$ 105,00 |
| Fev | R$ 5,25 | R$ 110,25 |
| Mar | R$ 5,51 | R$ 115,76 |
| Abr | R$ 5,79 | R$ 121,55 |
A cada mês, com exceção do primeiro, o rendimento de 5% não era sobre o capital inicial investido (R$ 100,00), mas sobre o montante do mês anterior.
Em fevereiro o rendimento foi calculado em 5% de R$ 105,00 = R$ 5,25. No total, o montante em fevereiro foi de R$ 110,25 (105 do mês anterior + o rendimento atual de 5,25).
Em março o rendimento foi calculado em 5% do montante de fevereiro (5% de R$ 110,25) = R$ 5,51 então o montante de março foi de R$ 110,25 + R$ 5,51 = R$ 115,76. No total, o investimento rendeu R$ 21,55 (R$ 1,55 a mais do que nos juros simples para essa aplicação). A conta fica:
$$\text{M} = \text{C} \cdot (1 + \text{i})^{\text{t}}$$
$$\text{M} = 100 \cdot (1 + 0.05)^{4} = 121.55 \text{ reais}$$
$$\text{J}_{\text{compostos}} = \text{M} - \text{C}$$
$$J = 121.55 - 100 = 21.55 \text{ reais}$$
Gráfico:
|
|
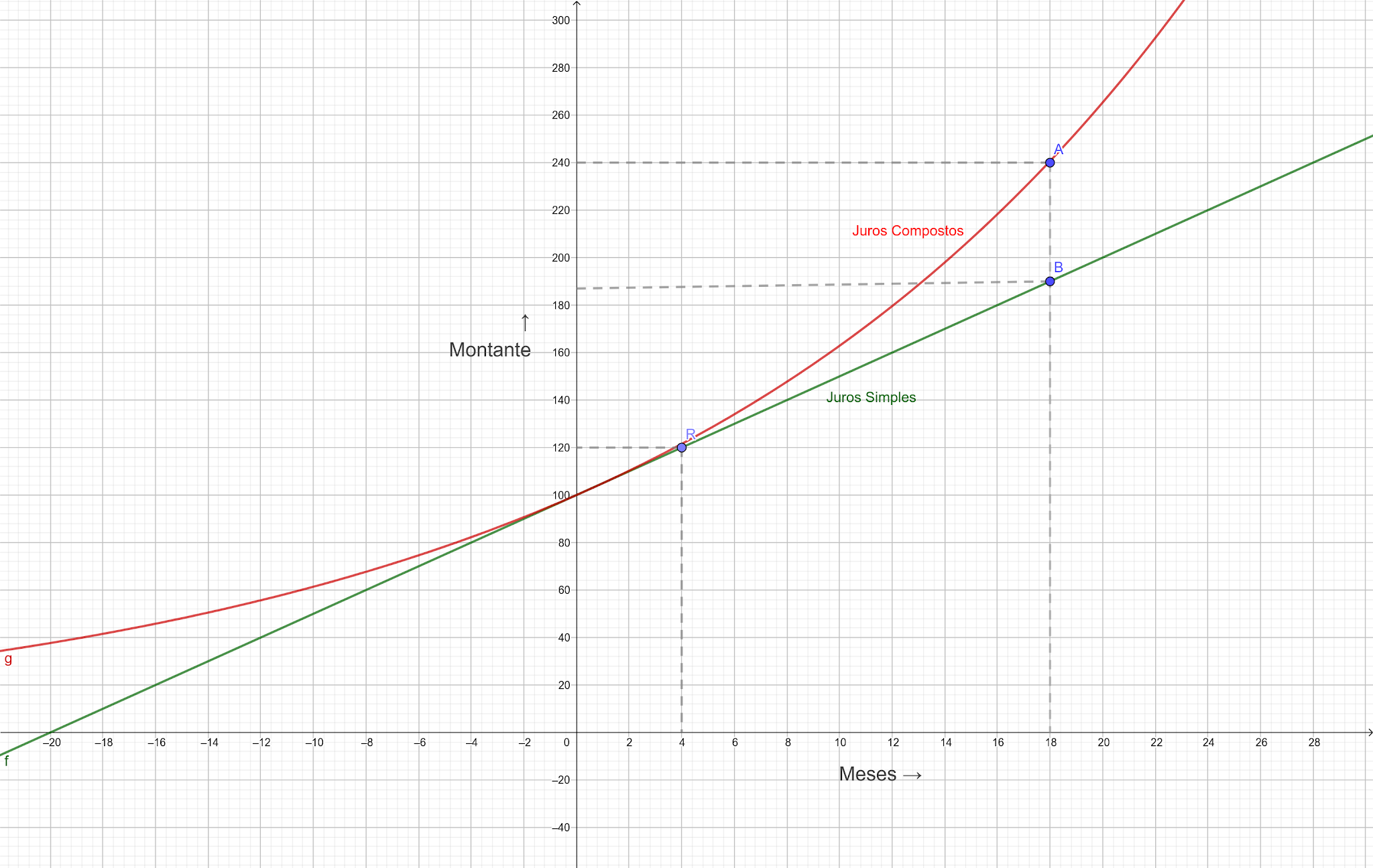
Gráfico representando as funções em juros simples e compostos |
Note que, graficamente, juros compostos formam uma função exponencial. E que,
a longo prazo, o rendimento se torna cada vez maior em relação a aplicação em
juros simples. Se a aplicação do investimento fosse feita durante 18 meses, em
juros simples haveria o retorno de R$ 190,00 (ponto B). E em juros compostos
seria de R$ 240,00 (ponto A), com uma diferença significativa entre os valores
encontrados em apenas 4 meses (próximo ao ponto R).
O número e (número de Euler)
O número de Euler, representado pela constante e, é um número irracional, encontrado de forma implícita e não intencional desde a Antiguidade, por meio de situações de ordem prática, segundo Pommer (2021).
$$e = 2.7182818284590452353...$$
Este valor foi melhor estudado graças aos trabalhos de Napier e Briggs com logaritmos, mas ficou conhecido mesmo por estudos em juros compostos, conforme explica O'Connor e Robertson (2001). Veremos a aplicação deste número em juros compostos para entendermos o limite fundamental exponencial, no próximo artigo.
Artigos:
Referência Bibliográfica
DICIONÁRIO PRIBERAM DA LÍNGUA PORTUGUESA. Consulte o significado / definição de juro no Dicionário Priberam da Língua Portuguesa, o dicionário online de português contemporâneo. Disponível em <https://dicionario.priberam.org/juro>. Acesso em 10 out. 2020.
POMMER, W.M. O número de euler: Possíveis abordagens no ensino básico. Seminários de Ensino de Matemática. Disponível em <https://www.nilsonjosemachado.net/sema20100831.pdf>. Acesso em 3 jan. 2021.
O‟CONNOR, J J; ROBERTSON, E.F. The number e. Setembro, 2001. Disponível
em: <http://www-history.mcs.st-andrews.ac.uk/HistTopics/e.html>. Acesso em 3 jan. 2021.
Para citar esse artigo:
 Pular para o conteúdo principal
Pular para o conteúdo principal

Comentários
Postar um comentário