Em artigos anteriores, conhecemos um pouco sobre o limite fundamental exponencial. Neste artigo, visitaremos mais um tipo de limite: o fundamental trigonométrico.
O limite fundamental trigonométrico é dado da seguinte forma:
$$\lim_{x \to 0} \frac{\sin(x)}{x} = 1$$ (sendo $$x$$ em radiano)
Neste artigo não faremos sua demonstração, mas resolveremos alguns exercícios
utilizando esse limite.
Exercícios
a) $$\lim_{x \to 0} \frac{\sin(3x)}{2x}$$
b) $$\lim_{x \to 0} \frac{\sin(3x)}{x}$$
c) $$\lim_{x \to 0} \frac{\sin(x)}{5x}$$
d) $$\lim_{x \to 0} \frac{\sin(\pi x)}{3\pi x}$$
Resolução
Agora veremos como resolver esses limites. O primeiro passo para resolver o
primeiro limite é multiplicá-lo por 1 $$\left(\frac{3}{3}\right)$$.
a) $$\lim_{x \to 0} \frac{\sin(3x)}{2x}$$ $$=$$ $$\lim_{x \to 0} \left(\frac{\sin(3x)}{2x} \cdot \frac{3}{3}\right)$$
3/3 é igual a 1, então não estamos alterando o resultado da nossa fração.
Agora, o próximo passo é reorganizar a fração em um novo produto.
$$\lim_{x \to 0} \left(\frac{3 \cdot \sin(3x)}{2 \cdot 3x}\right)$$ $$=$$ $$\lim_{x \to 0} \left(\frac{3}{2} \cdot \frac{\sin(3x)}{3x}\right)$$
Pela
propriedade dos limites, o limite de um produto é igual ao produto dos limites. Então nossa
equação fica assim:
$$\lim_{x \to 0} \left(\frac{3}{2}\right) \cdot \lim_{x \to 0} \left(\frac{\sin(3x)}{3x}\right)$$
Sabemos que o limite de uma função constante é igual a própria constante,
logo:
$$\frac{3}{2} \cdot \left(\lim_{x \to 0} \frac{\sin(3x)}{3x}\right)$$ $$=$$ $$\frac{3}{2} \cdot 1 = \frac{3}{2}$$
Gráfico de função
|
| Quando o limite de f(x) tende a 0, f(x) se aproxima de 1,5. |
Nas demais resoluções aplicaremos a mesma ideia.
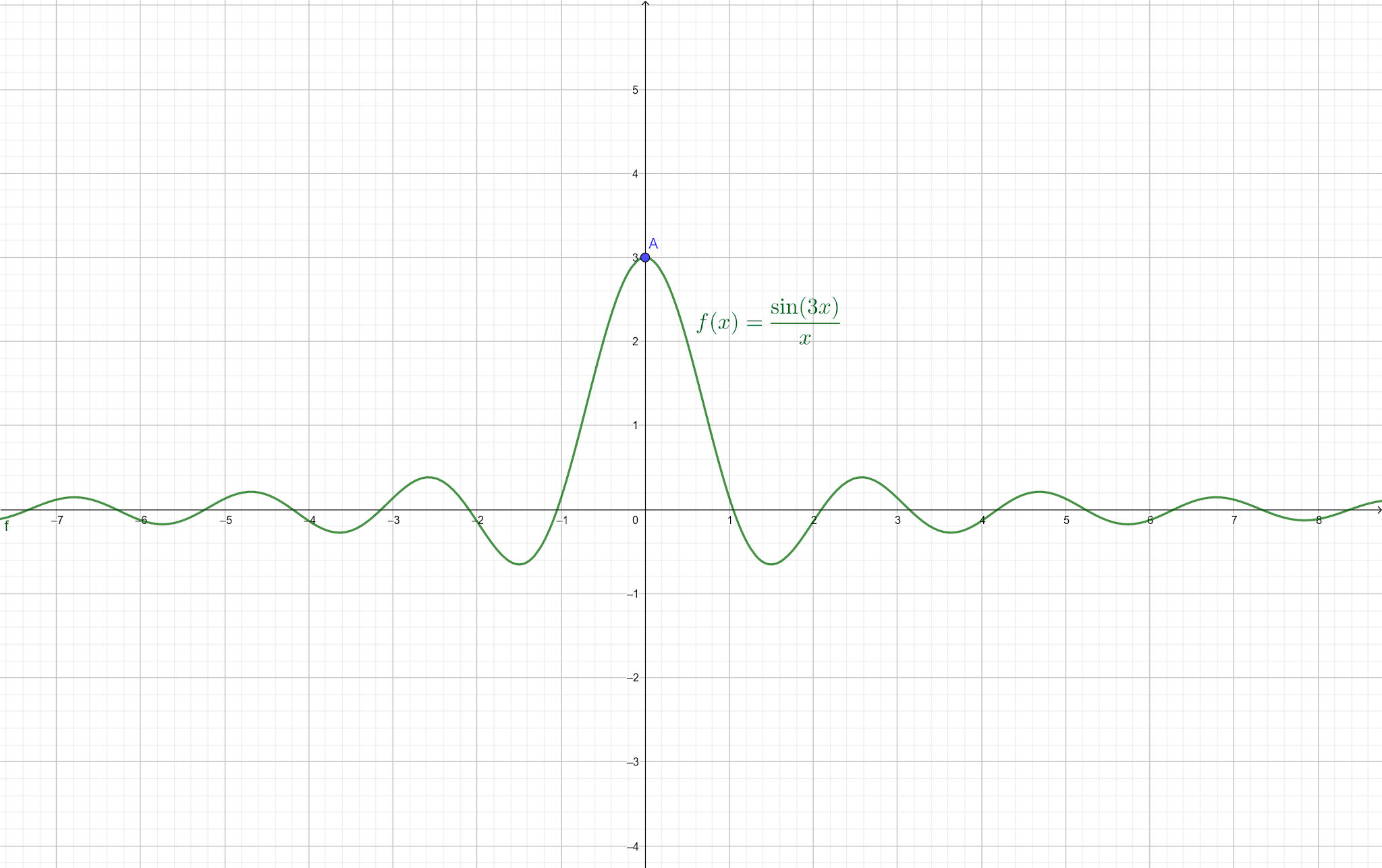
b) $$\lim_{x \to 0} \frac{\sin(3x)}{x}$$ $$=$$ $$\lim_{x \to 0} \left(\frac{\sin(3x)}{x} \cdot \frac{3}{3}\right)$$ $$=$$ $$3 \cdot \lim_{x \to 0} \left(\frac{\sin(3x)}{3x}\right)$$ $$=$$ $$3$$
Gráfico da função
|
|
Quando o limite de f(x) tende a 0,
f(x) se aproxima de 3. |
c) $$\lim_{x \to 0} \frac{\sin(x)}{5x}$$ $$=$$ $$\lim_{x \to 0} \left(\frac{\sin(x)}{x}\cdot \frac{1}{5}\right)$$ $$=$$ $$\frac{1}{5} \cdot \lim_{x \to 0} \frac{\sin(x)}{x}$$ $$=$$ $$\frac{1}{5}$$
Gráfico da função
|
| Quando o limite de f(x) tende a 0, f(x) se aproxima de 0,2. |
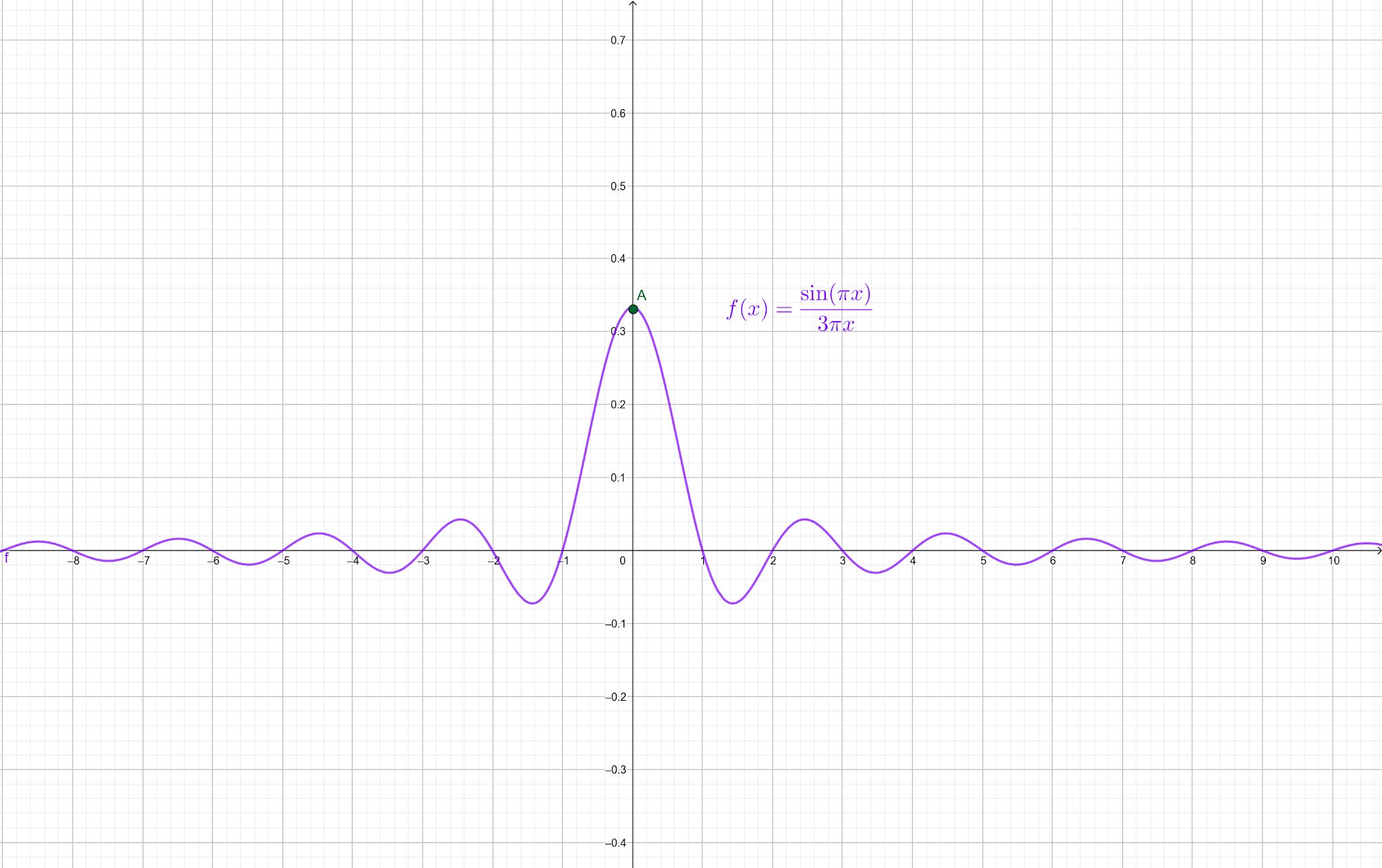
d) $$\lim_{x \to 0} \frac{\sin(\pi x)}{3\pi x}$$ $$=$$ $$\lim_{x \to 0}
\left(\frac{\sin(\pi x)}{\pi x} \cdot \frac{1}{3}\right)$$ $$=$$
$$\frac{1}{3} \cdot \lim_{x \to 0} \frac{\sin(\pi x)}{\pi x}$$ $$=$$
$$\frac{1}{3}$$
Gráfico da função
|
|
| Quando o limite de f(x) tende a 0, f(x) se aproxima de 0,333.... |
- $$x = 1 \Rightarrow n = 3$$
- $$x = 0.1 \Rightarrow n = 0.3$$
- $$x = 0.01 \Rightarrow n = 0.03$$
- ...
- $$x \to 0 \Rightarrow n \to 0$$
Para citar esse artigo:
Comentários
Postar um comentário