Na série de exercícios sobre limites de funções polinomiais com X tendendo a ±
infinito vimos algumas propriedades dos limites. Neste artigo você poderá
conhecer mais detalhadamente quais são essas propriedades e suas regras de
aplicação.
Índice
Limite de uma Constante
Propriedade:
$$\lim_{x \to a} c = c$$
Exemplo:
$$\lim_{x \to 2} 3 = 3$$
Gráfico do Exemplo
|
|
f(x) = 3 |
Propriedade:
$$\lim_{x \to a} [f(x) + g(x)]$$ $$=$$ $$\lim_{x \to a} f(x) + \lim_{x \to a}
g(x)$$
Exemplo:
$$\lim_{x \to 5} (x² + 2x)$$ $$=$$ $$\lim_{x \to 5} (x²) + \lim_{x \to 5}
(2x)$$ $$=$$ $$25 + 10 = 35$$
Gráfico do Exemplo
|
|
h(5) = (5²) + (2 × 5) = 25 + 10 = 35 |
Limite da Diferença
Propriedade:
$$\lim_{x \to a} [f(x) - g(x)]$$ $$=$$ $$\lim_{x \to a} f(x) - \lim_{x \to
a} g(x)$$
Exemplo:
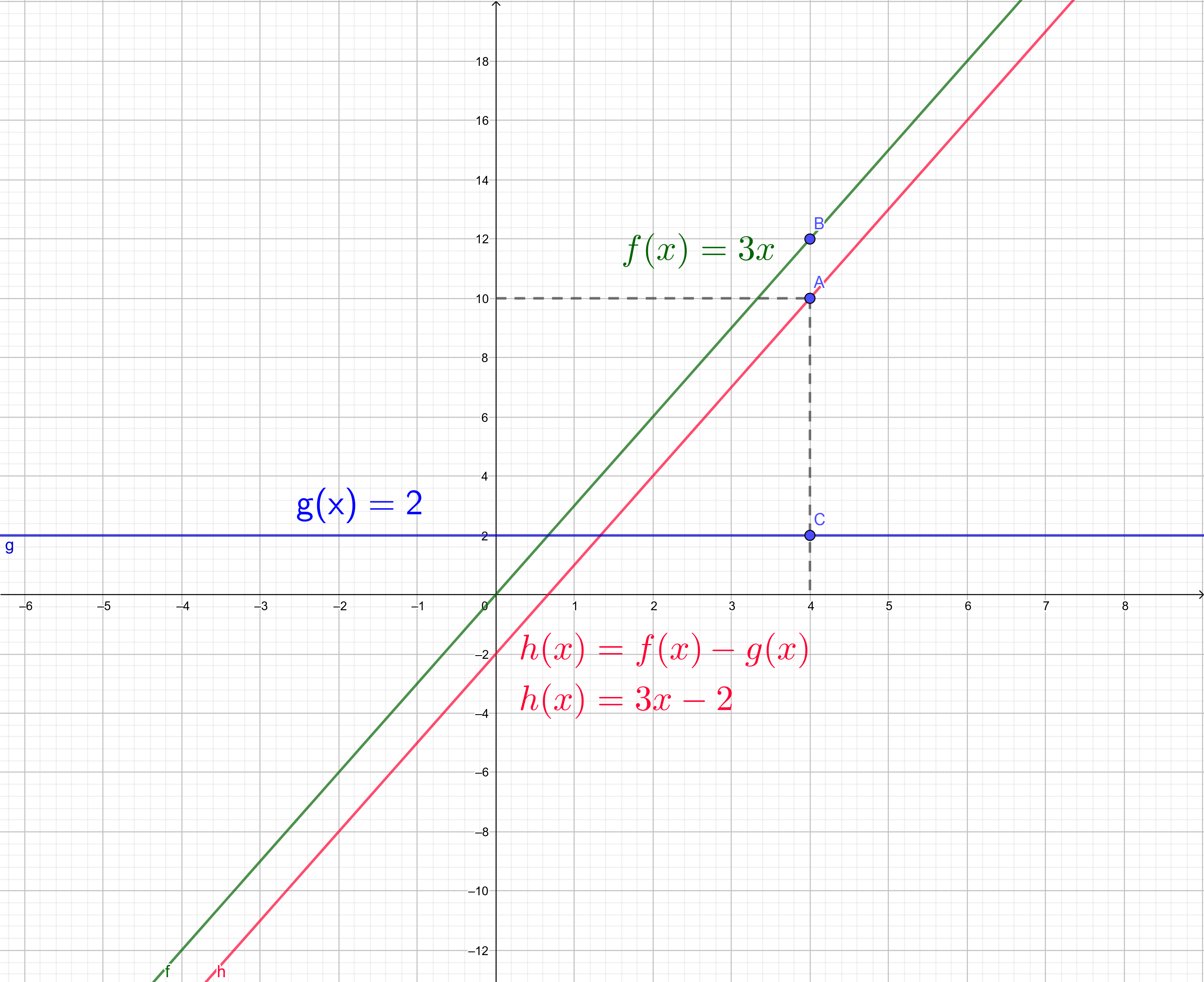
$$\lim_{x \to 4} (3x - 2)$$ $$=$$ $$\lim_{x \to 4} (3x) - \lim_{x \to 4}
(2)$$ $$=$$ $$12 - 2 = 10$$
Gráfico do Exemplo
|
|
h(4) = (3 × 4) - 2 = 12 - 2 = 10 |
Limite do Produto
Propriedade:
$$\lim_{x \to a} [f(x) \cdot g(x)]$$ $$=$$ $$\lim_{x \to a} f(x) \cdot
\lim_{x \to a} g(x)$$
Exemplo:
$$\lim_{x \to 5} (2x \cdot 4x)$$ $$=$$ $$\lim_{x \to 5} (2x) \cdot
\lim_{x \to 5} (4x)$$ $$=$$ $$(2 \times 5) \cdot (4 \times 5)$$ $$=$$
$$10 \cdot 20 = 200$$
Gráfico do Exemplo
|
|
h(5) = (2 × 5) · (4 × 5) = 10 · 20 = 200 |
Uma outra propriedade associada a constantes e produtos é:
$$\lim_{x \to a} (c f(x)) = c \cdot \lim_{x \to a} f(x)$$
Exemplo:
$$\lim_{x \to 5} (2x^{3})$$ $$=$$ $$2 \cdot \lim_{x \to 5} (x^{3})$$
$$=$$ $$2 \cdot 125 = 250$$
Limite do Quociente
Propriedade:
$$\lim_{x \to a} \left[\frac{f(x)}{g(x)}\right]$$ $$=$$ $$\frac{\lim_{x
\to a} f(x)}{\lim_{x \to a} g(x)}$$ se $$\lim_{x \to a} g(x) \not=
0$$
Exemplo:
$$\lim_{x \to 2} \left[\frac{x^2}{2x}\right]$$ $$=$$ $$\frac{\lim_{x \to
2} x^2}{\lim_{x \to 2} 2x}$$ $$=$$ $$\frac{2^{2}}{2 \cdot 2}$$ $$=$$
$$\frac{4}{4} = 1$$
Gráfico do Exemplo
|
|
h(2) = (2²)/(2·2) = 4/4 = 1 |
Limite de uma Potência
Propriedade:
$$\lim_{x \to a} [f(x)]^{n} = [\lim_{x \to a} f(x)]^{n}$$
Exemplo:
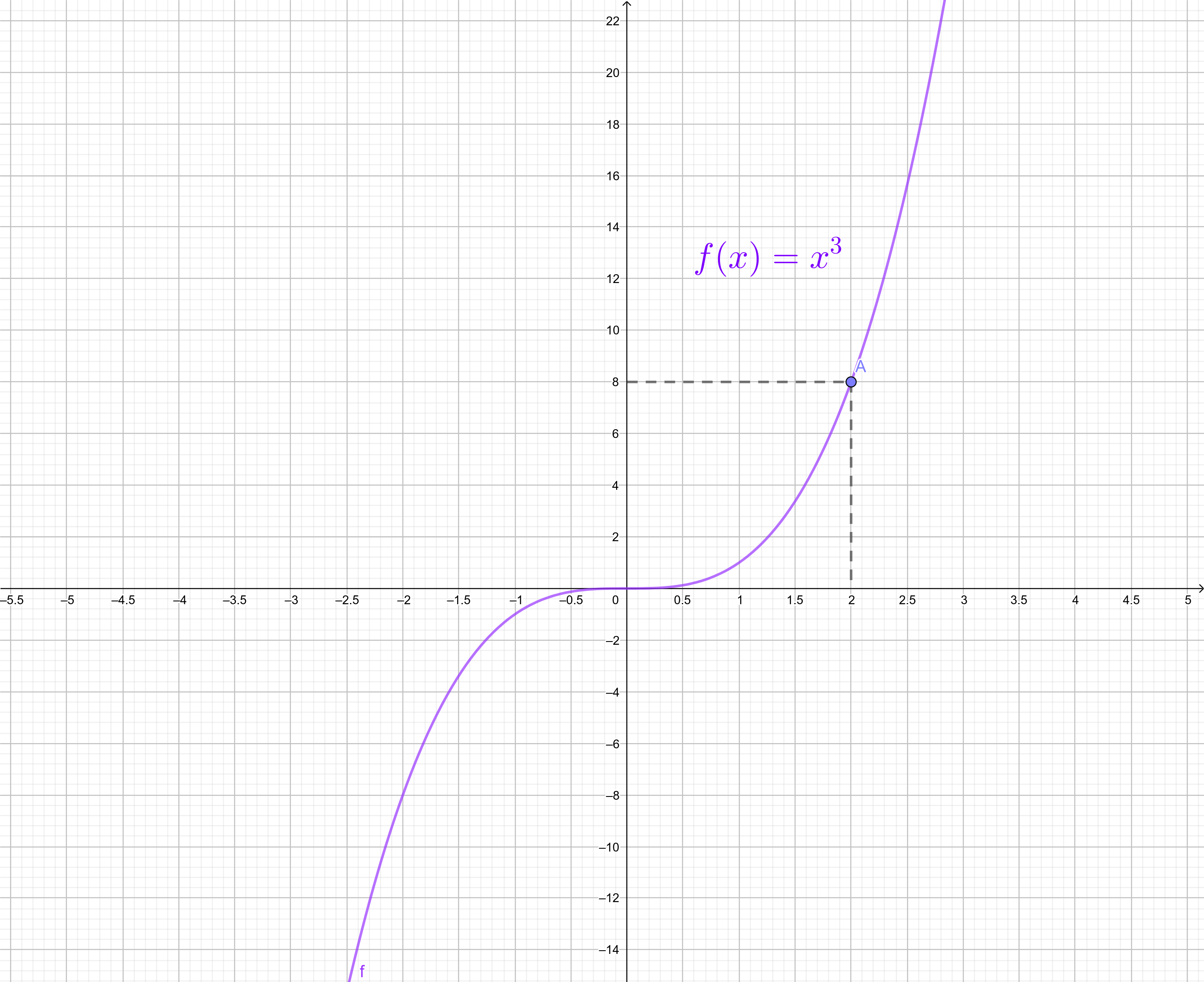
$$\lim_{x \to 2} (x^{3}) = [\lim_{x \to 2} (2)]^{3}$$ $$=$$ $$2^{3} = 8$$
Gráfico do exemplo
|
|
f(2) = 2³ = 8 |
Limite de uma Raiz
Propriedade:
$$\lim_{x \to a} \sqrt[n]{f(x)} = \sqrt[n]{\lim_{x \to a} f(x)}$$ sendo
$$n \in \mathbb{N}^{*}$$
Exemplo:
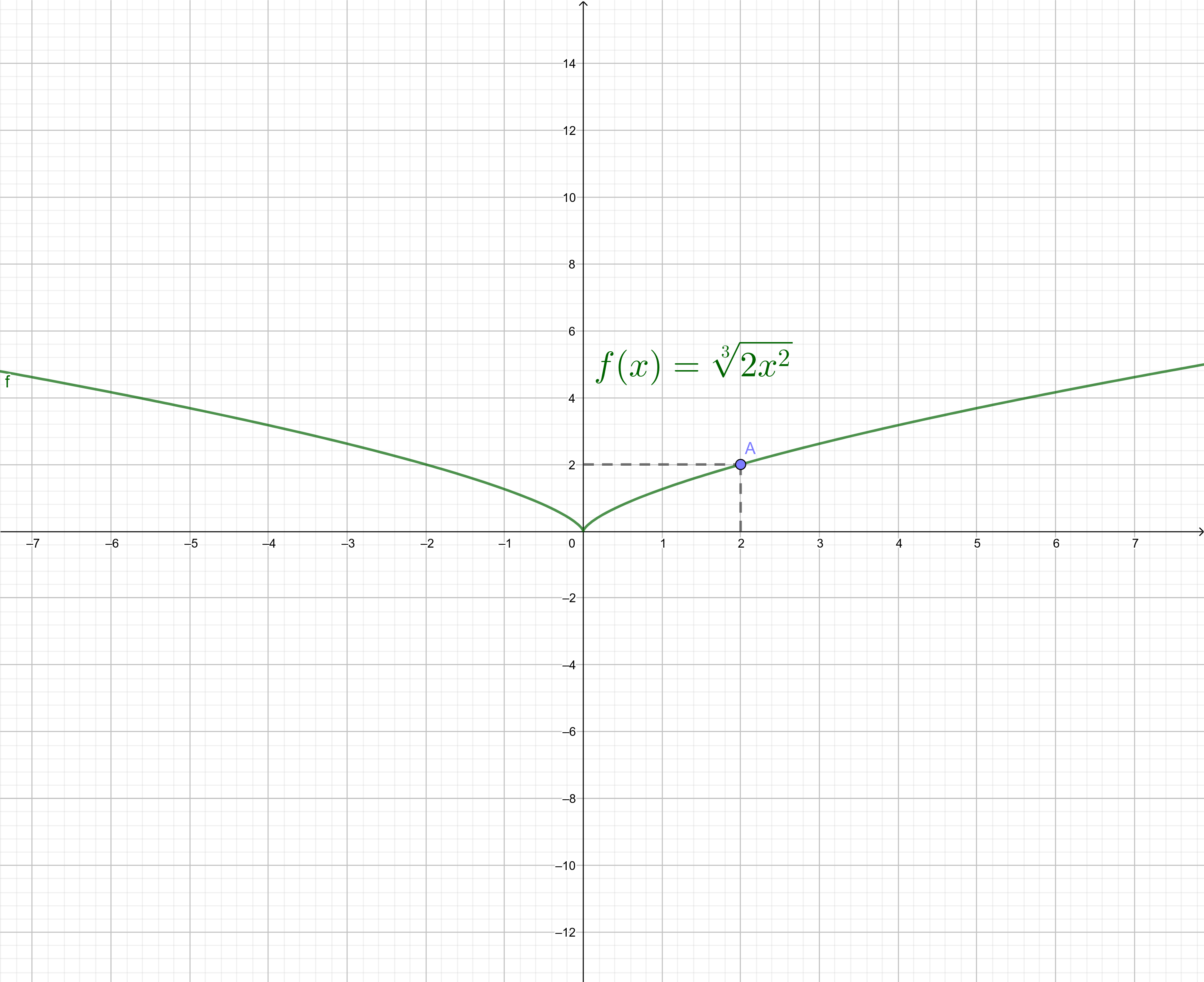
$$\lim_{x \to 2} \sqrt[3]{2x^{2}} = \sqrt[3]{\lim_{x \to 2} 2x^{2}}$$
$$=$$ $$\sqrt[3]{2 \cdot 2^{2}} = \sqrt[3]{2 \cdot 4}$$ $$=$$
$$\sqrt[3]{8}$$ $$=$$ $$\sqrt[3]{2^{3}} = 2$$
Gráfico do Exemplo
|
|
f(2) = ³√(2 · 2²) = ³√(2 · 4) = ³√(8) = ³√(2³) = 2 |
Limite de uma Função Composta
Propriedade:
$$\lim_{x \to a} g(f(x)) = g(\lim_{x \to a} f(x))$$
Exemplo:
$$\lim_{x \to 10} [\log_{10} (100x)]$$ $$=$$ $$\log_{10} [\lim_{x \to 10}
(100x)]$$ $$=$$ $$\log_{10} (1000) = 3$$
Gráfico do Exemplo
|
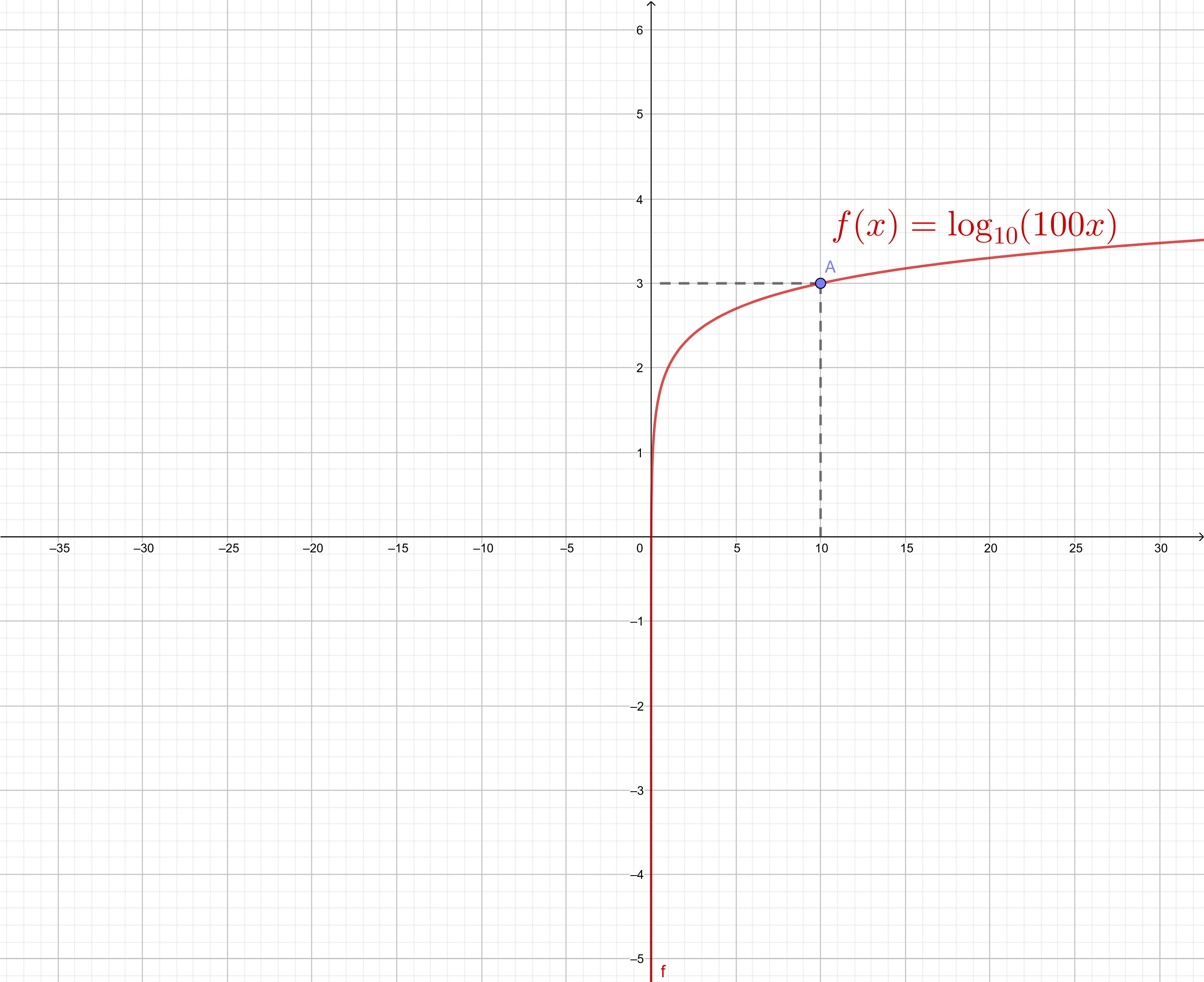
| f(10) = log(100 · 10) = log(1000) = 3 |
Limite de uma Função Exponencial
Propriedade:
$$\lim_{x \to a} b^{f(x)} = b^{\lim_{x \to a} f(x)}$$
Exemplo:
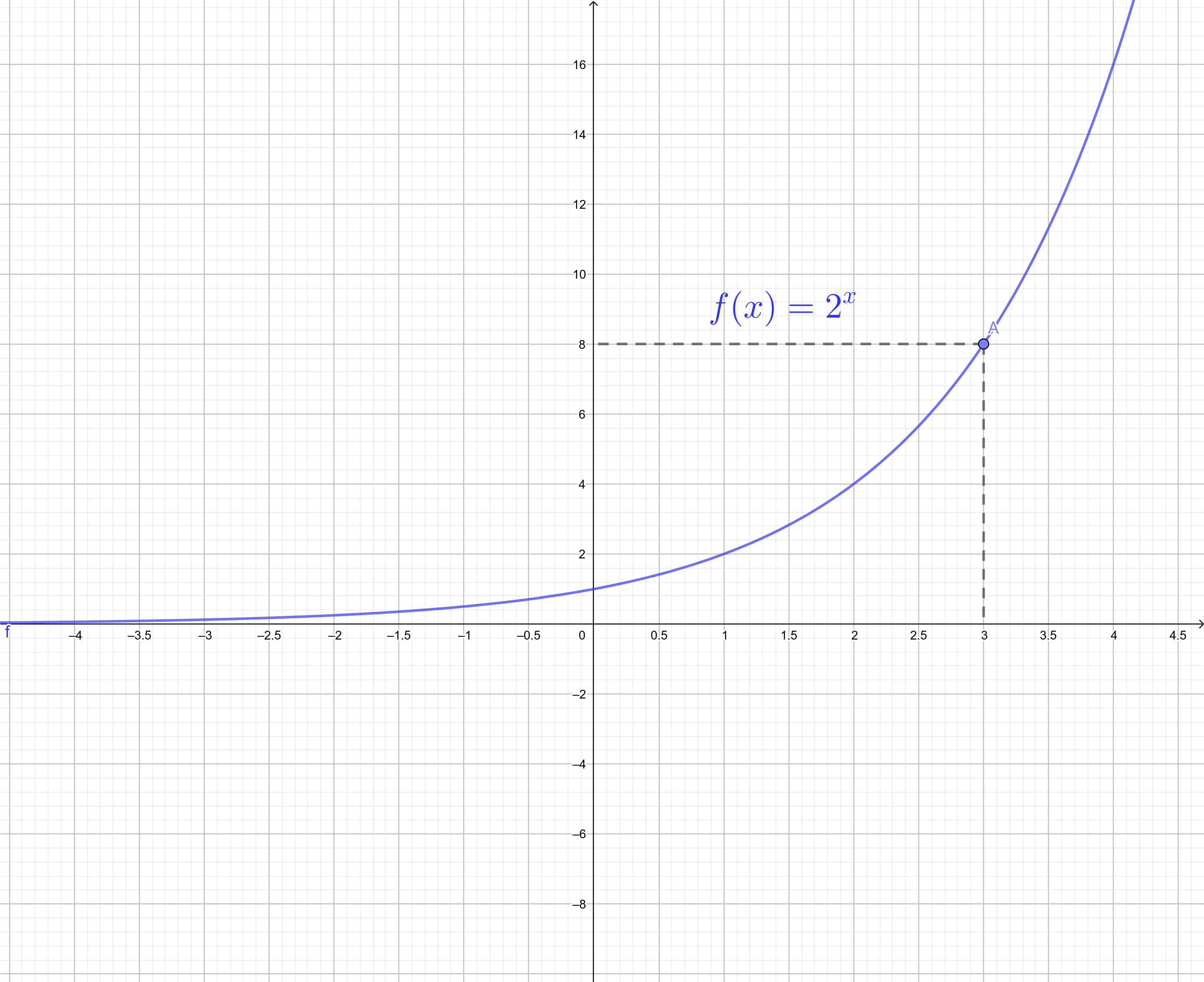
$$\lim_{x \to 3} 2^{x} = 2^{\lim_{x \to 3} x} = 2^{3} = 8$$
Gráfico do Exemplo
|
|
f(3) = 2³ = 8 |
Artigos
Referência Bibliográfica
MORETTIN, P. A.; HAZZAN, S.; BUSSAB, W. O.
Introdução ao Cálculo para Administração, Economia e Contabilidade. 1. ed. São Paulo: Saraiva, 2009. 342 p.
STEWART, J. Cálculo volume I. 6 ed. São Paulo: Cengage Learning,
2011. 532 p.
Para citar esse artigo:
Comentários
Postar um comentário