 |
| Lógica Proposicional - Árvore de Composição e Decomposição de uma Fórmula |
Vimos a definição e aprendemos a criar uma fórmula no artigo
Lógica Proposicional - Fórmulas Atômicas e Complexas. Com isso, podemos esquematizá-la no que chamamos
árvore de formação de fórmulas.
Inicialmente, observemos a primeira linha (de cima pra baixo) da imagem
"Árvore de composição e decomposição de uma fórmula". Partimos das sentenças
$$\text{A, B, C}$$ e $$\text{D}$$, que constituem a primeira regra da
definição de fórmula.
Observemos a segunda linha e aplicando a segunda regra da definição de
fórmula, foi obtido as fórmulas: $$(\neg$$$$\text{A})$$, $$(\text{A}$$
$$\rightarrow$$ $$\text{B})$$, $$(\text{B}$$ $$\wedge$$ $$\text{C})$$,
$$(\text{C}$$ $$\vee$$ $$\text{D})$$ e $$(\text{D}$$ $$\leftrightarrow$$
$$\text{D})$$.
A terceira linha recebeu a aplicação da segunda regra da definição, assim como
a segunda, e obtemos novas fórmulas: $$(\neg$$$$(\neg$$$$\text{A}))$$,
$$((\text{A}$$ $$\wedge$$ $$(\text{B}$$ $$\wedge$$ $$\text{C}))$$,
$$((\text{C}$$ $$\vee$$ $$\text{D})$$ $$\rightarrow$$ $$(\text{B}$$ $$\wedge$$
$$\text{C}))$$ e $$(\neg$$$$(\text{D}$$ $$\leftrightarrow$$ $$\text{D}))$$.
Observação importante: é muito importante aplicar corretamente a regra
de formação de fórmulas.
A verificação cuidadosa da formação de fórmula, nos permite analisar,
imediatamente, como uma fórmula foi obtida.
Vamos exibir um processo gráfico para determinar todas as subfórmulas de uma
fórmula. Tal processo faz uso de uma estrutura, muito utilizada na área da
computação, chamada árvore.
Subfórmulas: todas as fórmulas que compõe a fórmula em questão.
O que é uma árvore?
Estaremos mais interessados em um certo tipo de árvore chamada
árvore binária, mas começaremos analisando árvores em geral antes de
entrarmos nela.
Uma árvore consiste em nós (ou vértices) conectados por
arestas (segmento de reta que "liga" os nós).
Árvores têm sindo estudadas extensivamente como entidades matemáticas
abstratas, portando, há uma grande quantidade de conhecimento teórico sobre
elas. Uma árvore é, na verdade, uma instância de uma categoria mais geral
chamada grafo, mas não precisaremos nos preocupar com isso.
|
| Grafo |
A seguir, apresentamos graficamente os componentes de uma árvore binária
qualquer, observamos que tal descrição, não tem nenhum caráter formal, é
apenas para nos familiarizarmos com os elementos dessa estrutura.
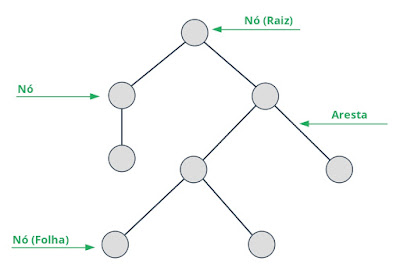
|
| Árvore Binária |
Acima está a representação gráfica de uma árvore binária genérica. Os vértices
(ou nós) são de três espécies, o nó a partir da qual toda árvore é gerada é
chamado de raiz, o nó terminal chamado de folha e os nós
intermediários chamados de nó interior. Toda árvore tem um começo
(raiz), meio (interior) e fim (terminal).
Aristóteles define que começo é aquilo que necessariamente não é antecedido
por nada, mas que pede ou produz, por natureza, um desdobramento; fim, ao
contrário, é aquilo que, por natureza, é antecedido por alguma coisa (da qual
decorre), mas que necessariamente não é seguido por mais nada; meio, por sua
vez, é aquilo que necessariamente segue e é seguido de outras coisas.
Chamamos de árvore binária, pois cada nó pode ter zero, um ou no máximo dois
filhos e podemos também classificar os nós como sucessores, aqueles que
vem abaixo, e ancestrais, aqueles que vem acima.
Árvore binária de uma sentença
Utilizaremos árvore binária do seguinte modo:
- Dada uma fórmula qualquer $$\text{P}$$ esta será a raiz da árvore de subfórmulas de $$\text{P}$$.
-
Se $$\text{P}$$ é uma fórmula do tipo não, então ela é composta por
uma fórmula $$\text{A}$$, de tal modo que $$\text{P}$$ $$\equiv$$
$$(\neg$$$$\text{A})$$. Logo, teremos:

Fórmula do tipo negação -
Se $$\text{P}$$ é uma fórmula do tipo conjunção, então ela é composta
por duas fórmulas $$\text{A}$$ e $$\text{B}$$, de tal modo que $$\text{P}$$
$$\equiv$$ $$(\text{A}$$ $$\wedge$$ $$\text{B})$$. Logo, teremos:

Fórmula do tipo conjunção -
Se $$\text{P}$$ é uma fórmula do tipo disjunção inclusiva, então ela
é composta por duas fórmulas $$\text{A}$$ e $$\text{B}$$, de tal modo que
$$\text{P}$$ $$\equiv$$ $$(\text{A}$$ $$\vee$$ $$\text{B})$$. Logo, teremos:

Fórmula do tipo disjunção inclusiva -
Se $$\text{P}$$ é uma fórmula do tipo disjunção exclusiva, então ela
é composta por duas fórmulas $$\text{A}$$ e $$\text{B}$$, de tal modo que
$$\text{P}$$ $$\equiv$$ $$(\text{A}$$ $$\veebar$$ $$\text{B})$$. Logo,
teremos:

Fórmula do tipo disjunção exclusiva -
Se $$\text{P}$$ é uma fórmula do tipo implicação, então ela é
composta por duas fórmulas $$\text{A}$$ e $$\text{B}$$, de tal modo que
$$\text{P}$$ $$\equiv$$ $$(\text{A}$$ $$\rightarrow$$ $$\text{B})$$. Logo,
teremos

Fórmula do tipo implicação -
Se $$\text{P}$$ é uma fórmula do tipo bi-implicação, então ela é
composta por duas fórmulas $$\text{A}$$ e $$\text{B}$$, de tal modo que
$$\text{P}$$ $$\equiv$$ $$(\text{A}$$ $$\leftrightarrow$$ $$\text{B})$$.
Logo, teremos:

Fórmula do tipo bi-implicação
Cada nó representa uma fórmula, em particular, cada nó gera uma sub-árvore.
Isto é, cada nó pode ser considerado uma raiz de uma árvore menor que tem como
nós os sucessores do respectivo nó raiz.
A construção de uma árvore de subfórmulas, a partir de uma fórmula dada,
termina quando todas as folhas contiverem somente letras proposicionais.
É muito importante ter em mente que uma fórmula é definida passo a passo e é
única a sua construção. Assim, por exemplo, podemos dizer qual conectivo foi
aplicado primeiro, o segundo, etc., até chegarmos ao último. Desse modo, é
possível decompor uma fórmula exibindo todas as suas subfórmulas que a compõe.
Este tema é de suma importância para a continuidade do aprendizado, convém
familiarizarmos mais de perto.
Analisemos a fórmula:
- $$[\text{A}$$ $$\rightarrow$$$$(\text{B}$$ $$\vee$$ $$\text{C})]$$
Para descobrir o último conectivo aplicado à fórmula, basta obedecer a regra
da aritmética básica. Na aritmética o operador mais externo será o último a
sofrer uma aplicação, no nosso caso o conectivo mais externo é o
$$\rightarrow$$, mas ao contrário da aritmética, onde o operado mais interno é
o primeiro a sofrer a aplicação, na árvore de composição e decomposição de uma
fórmula proposicional é o
operador mais externo que sofrerá a aplicação inicial.
Observação importante: sentenças, fórmulas ou proposições representam
a mesma coisa. Alguns livros usam sentenças, outros fórmulas e outros
proposições, mas no nosso caso usaremos todos para que o leitor vá se
familiarizando com as variações.
Após descobrirmos o conectivo mais externo, devemos ver se ele é um conectivo
binário ou unário. Entre os seis conectivos da lógica, o único unário é o
$$\neg$$, porque os demais ligam duas sentenças, enquanto o $$\neg$$ apenas
muda o valor verdade de uma. Como o último conectivo da fórmula em questão é
binário, então devermos traçar duas arestas. Logo, teremos:
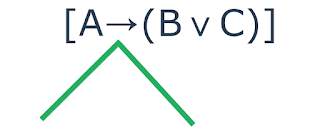 |
| Decomposição de uma fórmula do tipo implicação |
Repare na imagem acima que foi feito duas arrestas e que ambas partem do
último conectivo, implicação. É de suma importância que as arestas partam de
seus respectivos conectivos para facilitar a compreensão da árvore, já que o
objeto da árvore de composição e decomposição de uma fórmula é facilitar a
compreensão da formula.
Após traçarmos as arestas devemos "descer" as sentenças restantes, no caso
serão descidos as preposições $$\text{A}$$ e $$(\text{B}$$ $$\vee$$
$$\text{C})$$, o par de símbolos auxilares, colchetes, mais externos não
descem e nem o conectivo origem, implicação, das arestas. Logo, teremos:
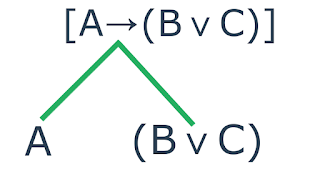
|
| Decomposição de uma fórmula do tipo implicação |
Repare que como a "quebra" ocorreu na implicação, apenas as duas fórmulas
ligadas por ela desceram e com isso foi resultado duas sentenças para se
trabalhar. Em casos assim, começamos, sempre, da esquerda para a direita.
A nossa primeira fórmula é $$\text{A}$$, mas reparem que ela é atômica
(desprovida de quaisquer conectivos) e neste caso não se tem o que fazer.
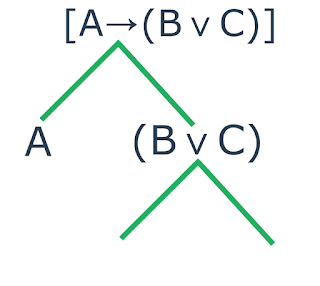
A segunda sentença é $$(\text{B}$$ $$\vee$$ $$\text{C})$$ e ao contrário da
primeira, ela é possuidora do conectivo $$\vee$$ e por isso ela sofrerá uma
aplicação. Logo, teremos:
|
| Decomposição de uma fórmula do tipo implicação |
Repare que a sentença $$(\text{B}$$ $$\vee$$ $$\text{C})$$ sofreu a mesma
aplicação que a $$[\text{A}$$ $$\rightarrow$$ $$(\text{B}$$ $$\vee$$
$$\text{A})]$$ e que a aresta que tem origem no conectivo $$\rightarrow$$ está
"conectada" no conectivo $$\vee$$, isso ocorre porque sempre devemos conectar
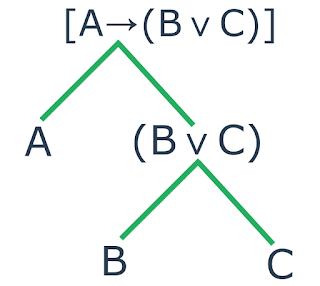
as arestas no próximo conectivo que sofrerá a "quebra". Logo, teremos:
|
| Decomposição de uma fórmula do tipo implicação |
Após a "quebra" do conectivo $$\vee$$ foram obtidas as sentenças $$\text{A}$$
e $$\text{B}$$ e repare que apenas eles desceram. Outra coisa que deve ser
reparada é que as arestas partem do $$\vee$$ e vão para as metas-variáveis e
como a árvore possui apenas letras, encerramos a decomposição.
Além de facilitar a compreensão de fórmulas grandes, a árvore nos retorna o
tipo da mesma. O tipo da fórmula é determinado pelo conectivo mais externo e
como na árvore é ele que sofre a primeira aplicação, então podemos concluir
que a fórmula trabalhada é do tipo
implicação.
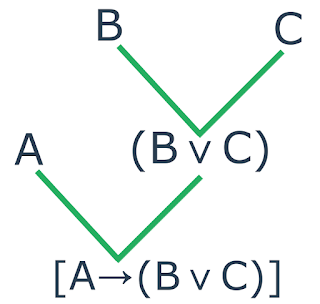
Se virarmos a árvore de cabeça para baixo, iremos adquirir a árvore de
composição. Vejamos:
|
| Composição de uma fórmula do tipo implicação |
Vejamos mais um exemplo:
- $$\{\neg$$$$[[(\neg$$$$\text{B})$$ $$\wedge$$ $$(\neg$$$$(\neg$$$$\text{A}))]$$ $$\leftrightarrow$$ $$[\neg$$$$(\neg$$$$(\text{B}$$ $$\vee$$ $$\text{C}$$$$))]]\}$$
Como saber a sequência em que foram aplicadas os conectivos? Sabemos que um
parênteses, colchetes e chaves à esquerda possui sempre um par à sua direita
correspondente. Podemos identificar isso de vários modos, porém há alguns
pares óbvios. Por exemplo, o par de chaves mais externo da fórmula:
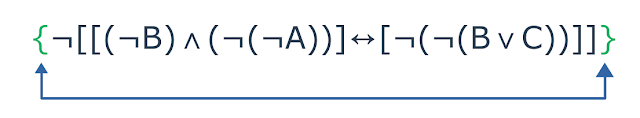
|
| Composição de uma fórmula do tipo negação |
Outros fáceis são os da negação de atômicas:
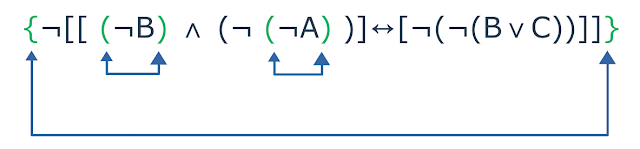
|
| Composição de uma fórmula do tipo negação |
E assim por diante:
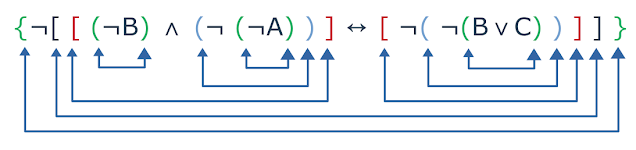
|
| Composição de uma fórmula do tipo negação |
Vemos que o $$\neg$$ foi o último conectivo aplicado a formula, porque ele é o
mais externo entre todos. Por conseguinte, o tipo desta fórmula é
negação. Com base no último conectivo iniciemos a nossa decomposição.
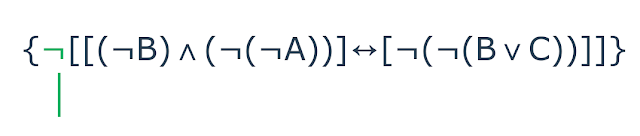
|
| Decomposição de uma fórmula do tipo negação |
Como o último conectivo é unário, $$\neg$$, fazemos uma aresta na vertical com
origem no $$\neg$$ e destino no próximo conectivo que sofrerá a quebra, no
caso o $$\leftrightarrow$$. Não podemos esquecer de descer as demais sentenças
com os seus respectivos conectivo. Vejamos:
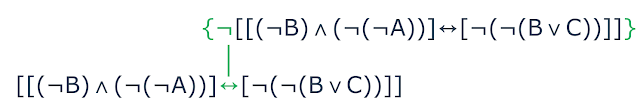
|
| Decomposição de uma fórmula do tipo negação |
A aplicação resultou na fórmula $$[[(\neg$$$$\text{B})$$ $$\wedge$$
$$(\neg$$$$(\neg$$$$\text{A}$$$$))]$$ $$\leftrightarrow$$
$$[\neg$$$$(\neg$$$$(\text{B}$$ $$\vee$$ $$\text{C}$$$$))]]$$ e como a aresta
está "conectada" no conectivo $$\leftrightarrow$$, aplicaremos a "quebra"
nele. Como ele é um conectivo binário, teremos duas arestas Vejamos:
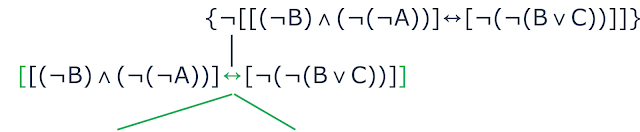
|
| Decomposição de uma fórmula do tipo negação |
Antes de descer as demais sentenças, devemos ver qual o conectivo mais externo
em cada uma.
Na sentença $$[(\neg$$$$\text{B})$$ $$\wedge$$
$$(\neg$$$$(\neg$$$$\text{A}$$$$))]$$ o conectivo mais externo é $$\wedge$$,
enquanto que na sentença $$[\neg$$$$(\neg$$$$(\text{B}$$ $$\vee$$
$$\text{C}$$$$))]$$ o conectivo mais externo é $$\neg$$. Com isso as arestas
estão ligadas a eles. Vejamos:
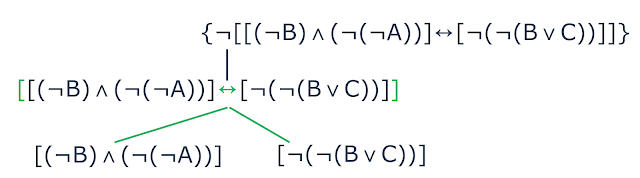
|
| Decomposição de uma fórmula do tipo negação |
Observando a imagem acima, vermos que os próximos conectivos a sofrer a quebra
são $$\wedge$$ e $$\neg$$. Vejamos:
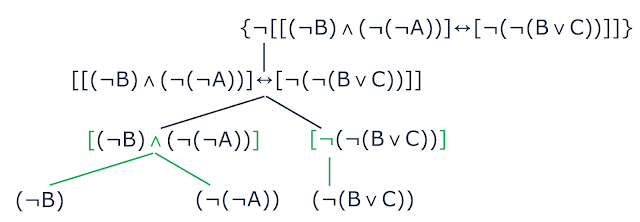
|
| Decomposição de uma fórmula do tipo negação |
Aplicando a mesma lógica, obteremos a seguinte árvore:
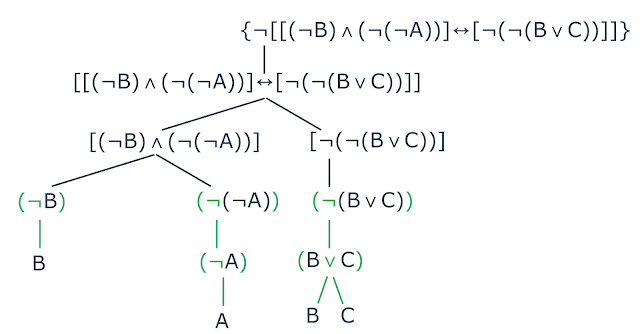
|
| Decomposição de uma fórmula do tipo negação |
Observação importante: não é necessário que a aresta que tem origem
no conectivo $$\neg$$ esteja na vertical, mas é necessário que ela tenha
final no próximo conectivo que sofrerá a quebra.
É de suma importância que o leitor tenha compreendido a formação de uma árvore
de composição e decomposição de uma fórmula, porque ela será frequentemente
usada. Caso tenha dúvida, faça um breve comentário que responderei assim que
possível.
E para finalizar, vejamos um exemplo que envolva conjuntos:
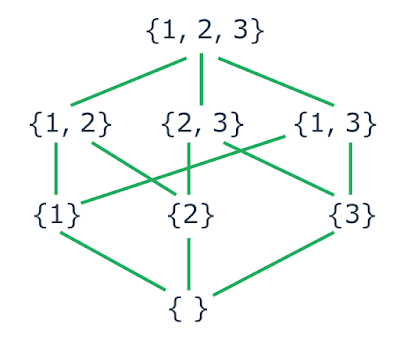
Seja P(A) = {{1}, {2}, {3}, {1,2}, {1 ,3}, {2, 3}, {1, 2, 3}, {}}. Represente
em um diagrama:
|
| Decomposição de um conjunto |
Caso o leitor tenha alguma dúvida sobre teoria dos conjuntos, clique
aqui.
O que você aprendeu
Este artigo serviu para demonstrar a criação de uma árvore de composição e
decomposição de uma fórmula com três exemplos, mostrou ela sendo aplicada na
teoria dos conjuntos e explico o que é uma árvore. Especificamente, você
aprendeu:
- O que é uma árvore.
- O que é uma árvore binária.
- Criação de uma árvore binária de composição e decomposição de uma fórmula.
- Aplicação em teoria dos conjuntos.
Continua em
Continuação de
Veja todos os artigos em
Lista de Artigos sobre Lógica Proposicional
Lista de Artigos sobre Lógica Proposicional
Referência Bibliográfica
ABE, J. M; SCALZITTI, A; FILHO, J. I. S.
Introdução à Lógica para a Ciência da Computação. 2. ed. São Paulo:
Arte & Ciência, 2002. 247 p.
GERSTING, A. L.
Fundamentos Matemáticos para a Ciência da Computação: um tratamento moderno
de matemática discreta. 5. ed. Rio de Janeiro: LTC, 2012. 597 p.
LAFORE, R. Estruturas de dados & algoritmos em Java. 2. ed. Rio de
Janeiro: Ciência Moderna, 2004. 702 p.
Para citar esse artigo:
 Pular para o conteúdo principal
Pular para o conteúdo principal
Faltou o par não-ordenado {1,3} em P(A).
ResponderExcluirOlá Victor Lennon, obrigado pela observação. Seu feedback é muito importante.
ExcluirAo autor; realmente um site sensacional, ótimas explicações!
ResponderExcluirOlá, muito obrigado pela comentário :) seja bem-vindo!
Excluir