No artigo anterior aprendemos sobre as
propriedades dos limites, que podem ser utilizadas na resolução matemática de limites finitos ou
infinitos. Neste novo tópico de estudo analisaremos a continuidade de uma
função e a sua relação com os limites.
Conceito
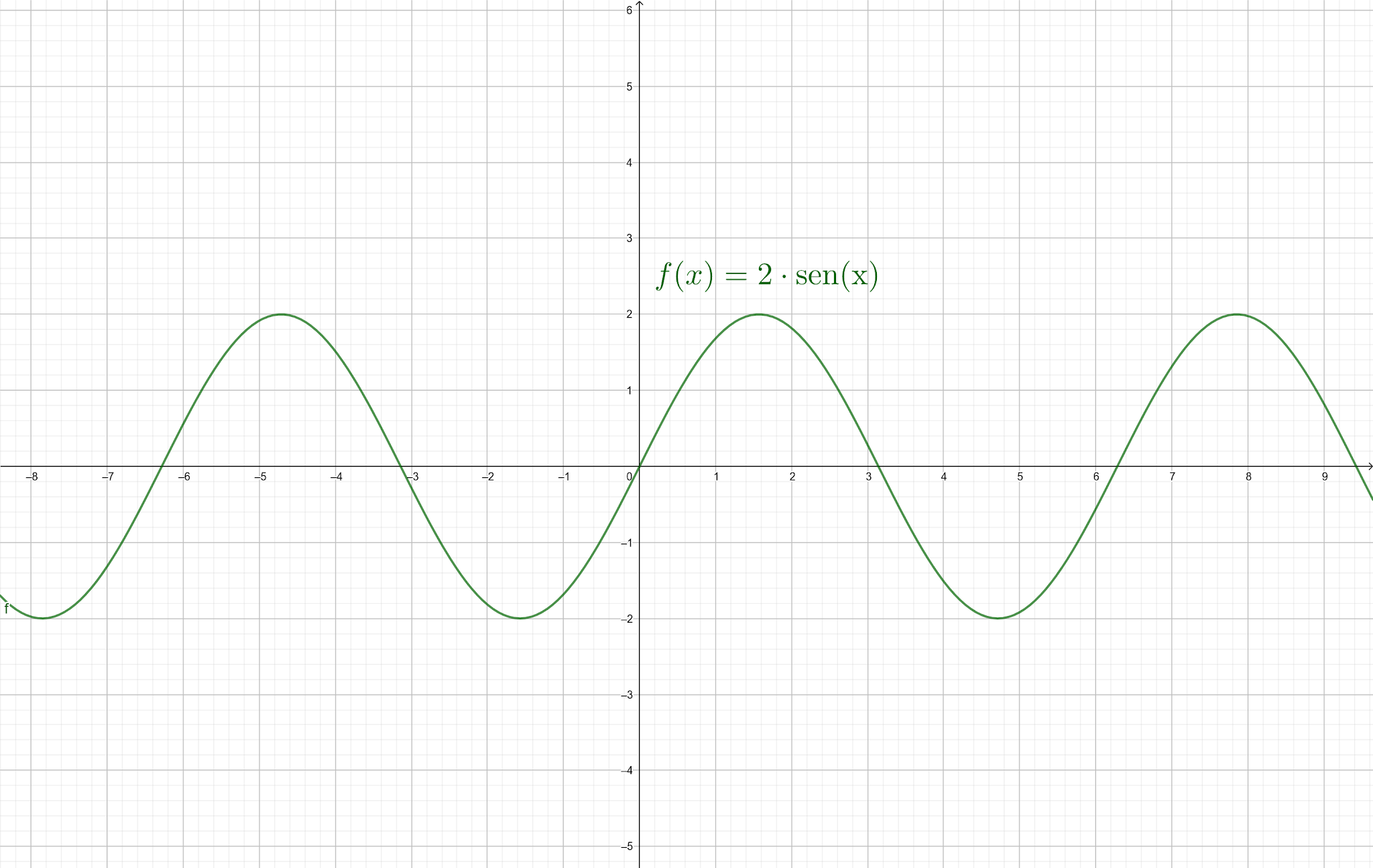
Intuitivamente, quando o gráfico de uma função não apresenta interrupções,
dizemos que ela é contínua.
|
|
Exemplo de Função Contínua f(x) = 2sen(x) |
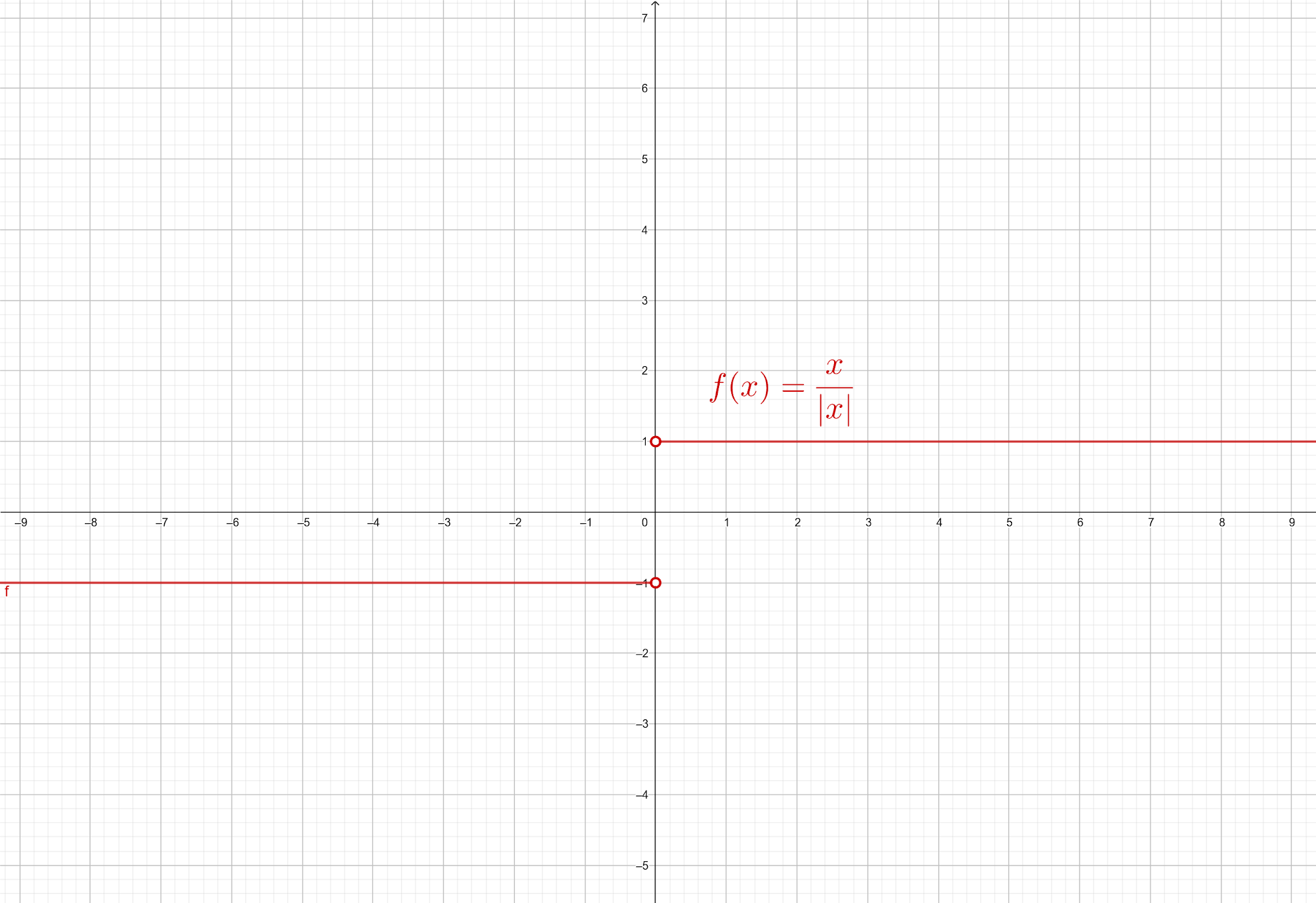
Se houver algum ponto onde ocorre a interrupção, dizemos que é um
ponto de descontinuidade.
|
|
Exemplo de Função Descontínua f(x) = x/|x| |
Definição
Se uma função tem limite em um ponto A e, além disso, é possível calcular o
valor dessa função no ponto e o valor coincide com o limite, podemos dizer que
a função é contínua nesse ponto.
Uma função f é contínua em um número a se:$$\lim_{x \to a} f(x) = f(a)$$
Essa definição requer implicitamente três condições para a continuidade de
f em a.
1. $$f(a)$$ está definida, ou seja, a está no domínio de
f.
2. $$\lim_{x \to a} f(x)$$ existe.
3. $$\lim_{x \to a} f(x) = f(a)$$
Note que $$\exists\lim_{x \to a} f(x)$$ se:
- $$\exists\lim_{x \to a^{+}} f(x)$$
- $$\exists\lim_{x \to a^{-}} f(x)$$
- $$\lim_{x \to a^{+}} f(x) = \lim_{x \to a^{-}} f(x)$$
Exemplos
Verificar a continuidade das funções:
a) $$f(x) = 4x + 1$$ no ponto $$x = 1$$
b) $$f(x) = \begin{cases} 2x + 3 \text{, se x} \not= \text{ 1}\\ 4
\text{, se x = 1}\end{cases}$$ no ponto $$x
= 1$$
c) $$f(x) = \begin{cases} x - 3 \text{, se x} \leq \text{ 1}\\ 1 - x
\text{, se x > 1}\end{cases}$$ no ponto $$x = 1$$
d) $$f(x) = \begin{cases} x^{2} - 1 \text{, se x < 2} \\ 7 - 2x \text{, se
x} \geq 2 \end{cases}$$ no ponto $$x = 2$$
Resolução
a) $$f(x) = 4x + 1$$ no ponto $$x = 1$$
1º verificando se existe $$f(a)$$ sendo $$a = 1$$.
$$f(1) = 4 \cdot 1 + 1 = 5$$
2º Verificando se existe o limite de $$f(x)$$ no ponto $$x = 1$$.
$$\lim_{x \to 1} (4x + 1) = 5$$
3º Verificando se $$f(a)$$ no ponto $$a = 1$$ é igual ao limite de $$f(x)$$ no
ponto $$x = 1$$.
$$\lim_{x \to 1} f(x) = f(1)$$
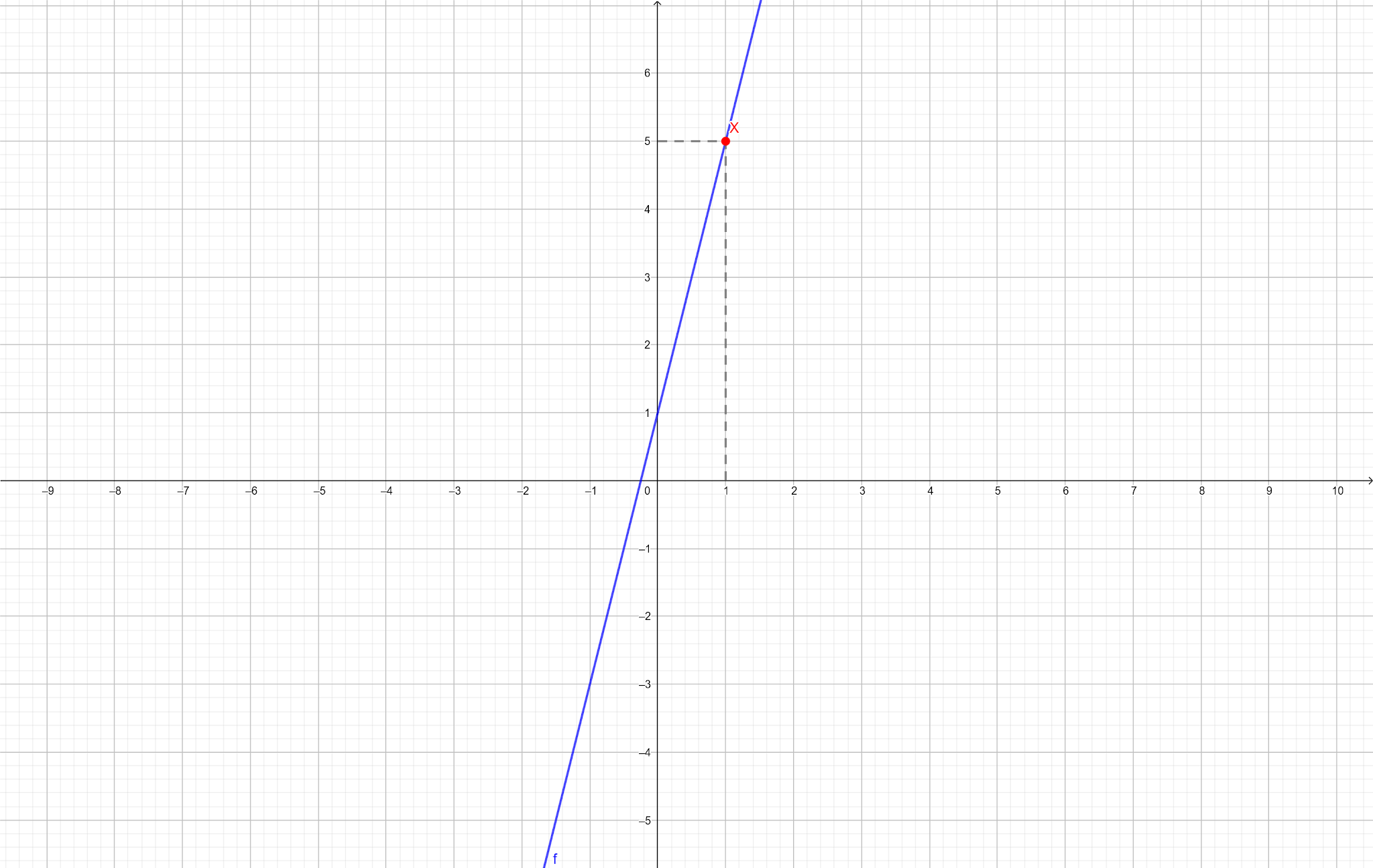
Gráfico
|
|
A função é contínua no ponto x = 1. |
Resposta: a função $$f(x)$$ é contínua no ponto $$x = 1$$.
b) $$f(x) = \begin{cases} 2x + 3 \text{, se x} \not= \text{ 1}\\ 4
\text{, se x = 1}\end{cases}$$ no ponto $$x
= 1$$
1º verificando se existe $$f(a)$$ sendo $$a = 1$$.
$$f(1) = 4$$
2º Verificando se existe o limite de $$f(x)$$ no ponto $$x = 1$$.
$$\lim_{x \to 1^{+}} (2x + 3) = 5$$
$$\lim_{x \to 1^{-}} (2x + 3) = 5$$
$$\lim_{x \to 1^{-}} (2x + 3)$$ $$=$$ $$\lim_{x \to 1^{+}} (2x + 3)$$
$$\therefore$$ $$\exists\lim_{x \to 1} (2x + 3) = 5$$
3º Verificando se $$f(a)$$ no ponto $$a = 1$$ é igual ao limite de $$f(x)$$ no
ponto $$x = 1$$.
$$f(1) \not= \lim_{x \to 1} (2x + 3) \therefore$$ $$f(x)$$ não é contínua no
ponto $$x = 1$$.
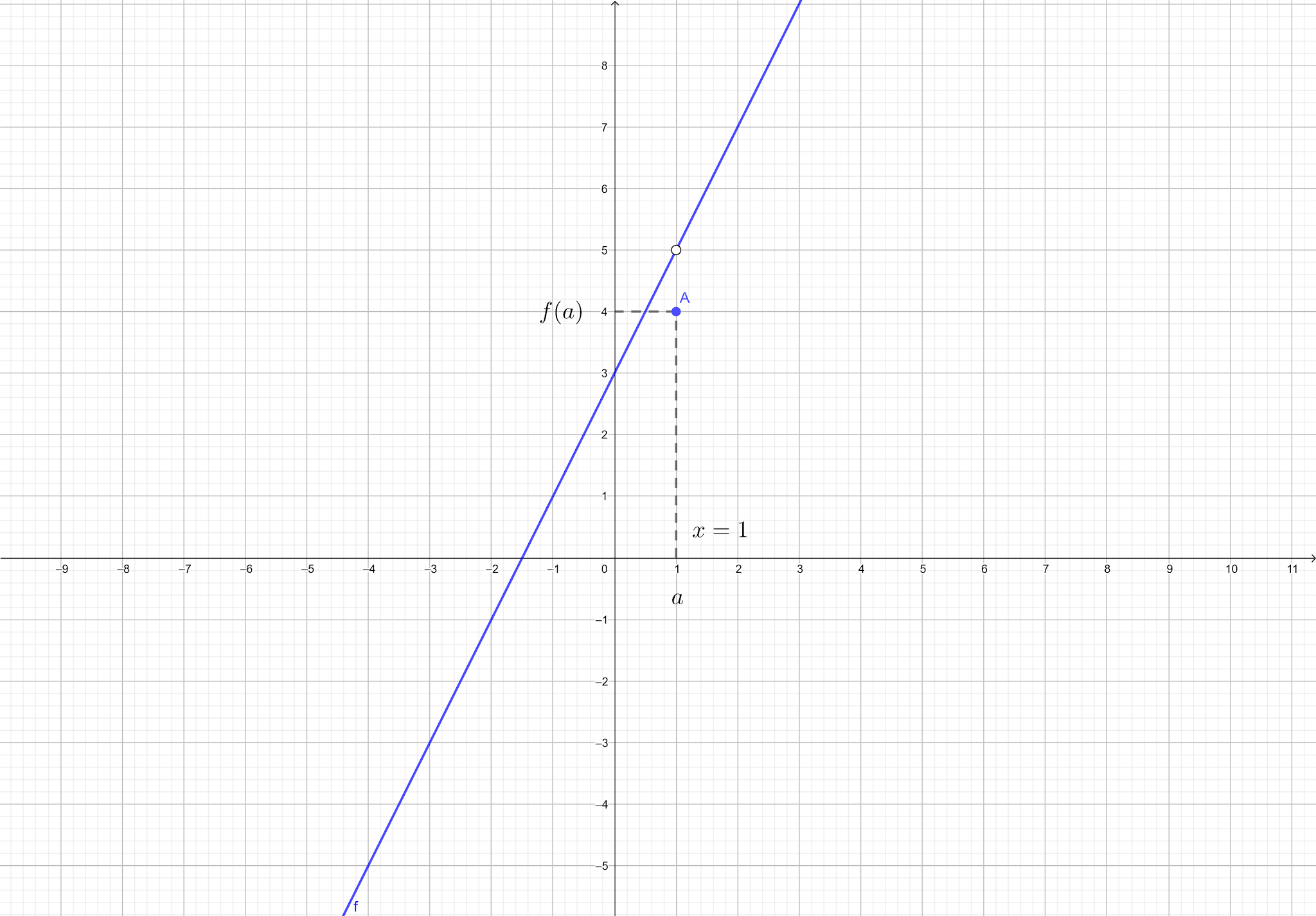
Gráfico
|
|
A função não é contínua no ponto x = 1 |
Resposta: a função $$f(x)$$ não é contínua no ponto $$x = 1$$.
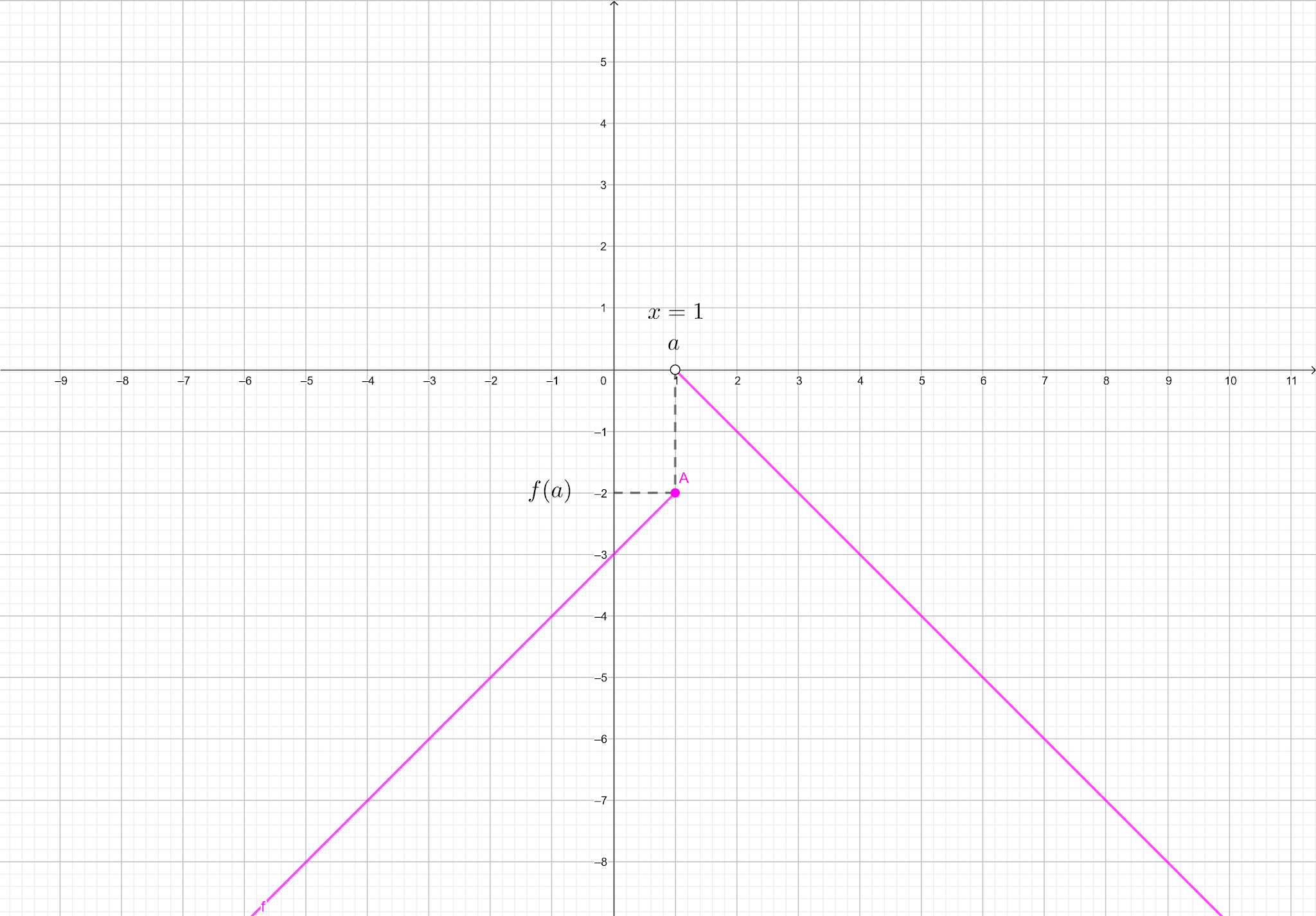
c) $$f(x) = \begin{cases} x - 3 \text{, se x} \leq \text{ 1}\\ 1 - x
\text{, se x > 1}\end{cases}$$ no ponto $$x = 1$$
1º verificando se existe $$f(a)$$ sendo $$a = 1$$.
$$f(1) = 1 - 3 = -2$$
2º Verificando se existe o limite de $$f(x)$$ no ponto $$x = 1$$.
$$\lim_{x \to 1^{-}} (x - 3) = 1 - 3 = -2$$
$$\lim_{x \to 1^{+}} (1 - x) = 1 - 1 = 0$$
$$\lim_{x \to 1^{-}} f(x)$$ $$\not=$$ $$\lim_{x \to 1^{+}} f(x)$$
$$\therefore$$ $$\not\exists \lim_{x \to 1} f(x)$$
Gráfico
|
|
A função não é contínua no ponto x = 1 |
Resposta: a função $$f(x)$$ não é contínua no ponto $$x = 1$$.
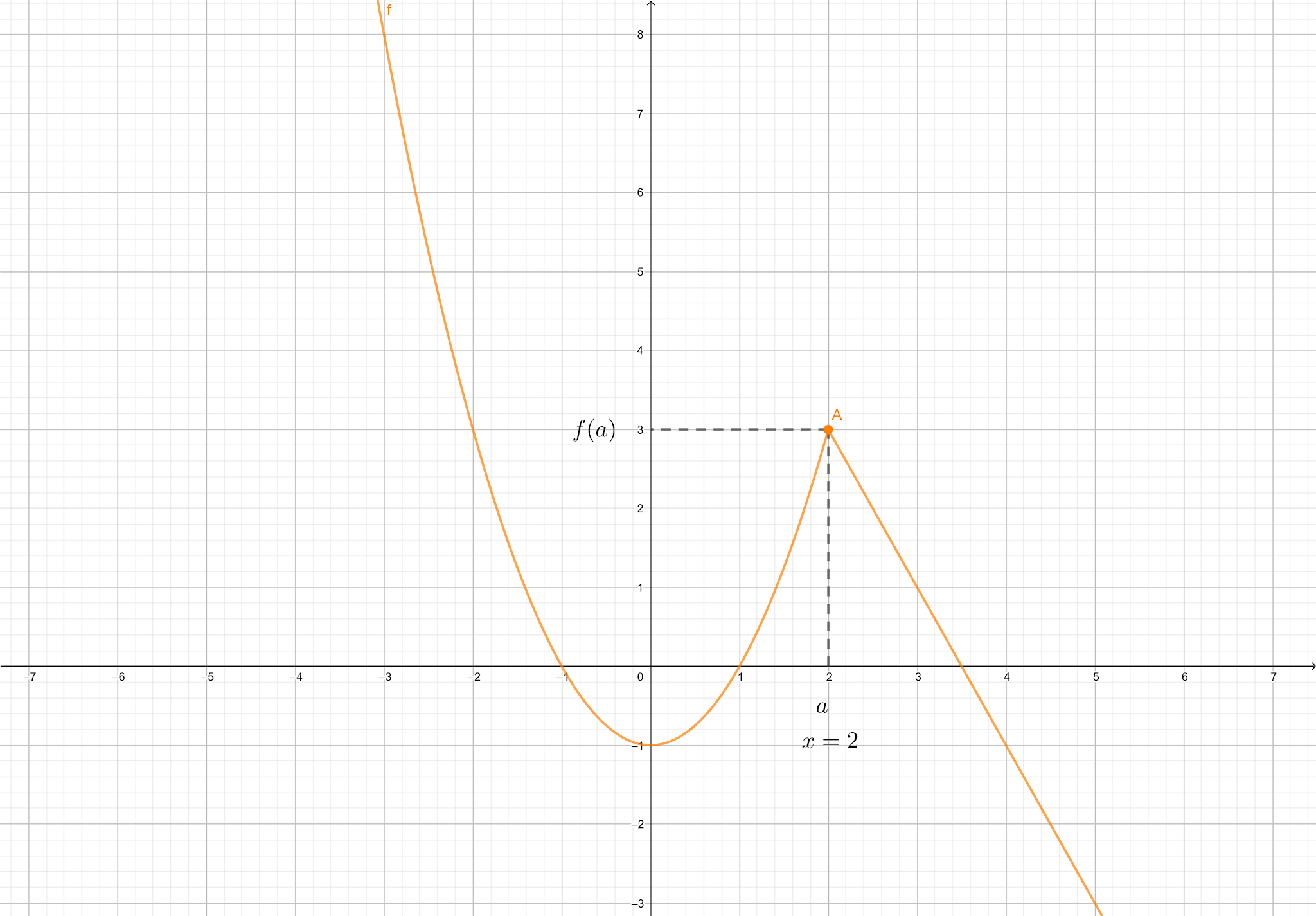
d) $$f(x) = \begin{cases} x^{2} - 1 \text{, se x < 2} \\ 7 - 2x \text{, se
x} \geq 2 \end{cases}$$ no ponto $$x = 2$$
1º verificando se existe $$f(a)$$ sendo $$a = 2$$.
$$f(2) = 7 - (2 \cdot 2) = 3$$
2º Verificando se existe o limite de $$f(x)$$ no ponto $$x = 2$$.
$$\lim_{x \to 2^{-}} (x^{2} - 1) = 2^{2} - 1 = 3$$
$$\lim_{x \to 2^{+}} (7 - 2x) = 7 - (2 \cdot 2) = 3$$
$$\lim_{x \to 2^{-}} f(x)$$ $$=$$ $$\lim_{x \to 2^{+}} f(x)$$ $$\therefore$$
$$\exists \lim_{x \to 2} f(x) = 3$$
3º Verificando se $$f(a)$$ no ponto $$a = 2$$ é igual ao limite de $$f(x)$$ no
ponto $$x = 2$$.
$$f(2) = \lim_{x \to 2} (7 - 2x) \therefore f(x)$$ é contínua no ponto $$x =
2$$.
Gráfico
|
|
A função é contínua no ponto x = 2 |
Resposta: a função $$f(x)$$ é contínua no ponto $$x = 2$$.
Estas foram as resoluções de exercícios envolvendo a continuidade de uma
função com limites. No próximo artigo veremos o cálculo do limite
fundamental exponencial.
Artigos
Referência Bibliográfica
MORETTIN, P. A.; HAZZAN, S.; BUSSAB, W. O. Introdução ao Cálculo para Administração, Economia e Contabilidade. 1. ed. São Paulo: Saraiva, 2009. 342 p.
STEWART, J. Cálculo volume I. 6 ed. São Paulo: Cengage Learning, 2011. 532 p.
MORETTIN, P. A.; HAZZAN, S.; BUSSAB, W. O. Introdução ao Cálculo para Administração, Economia e Contabilidade. 1. ed. São Paulo: Saraiva, 2009. 342 p.
STEWART, J. Cálculo volume I. 6 ed. São Paulo: Cengage Learning, 2011. 532 p.
Para citar esse artigo:
 Pular para o conteúdo principal
Pular para o conteúdo principal
Comentários
Postar um comentário