No artigo anterior em Teoria dos Conjuntos - Introdução vimos que é possível um conjunto estar contido dentro de outro conjunto. E essa relação é análoga ao nosso mundo real. Neste artigo veremos o que são subconjuntos e suas propriedades, bem como as operações que são estabelecidas entre eles.
Índice
Relação de Inclusão
Suponhamos um conjunto chamado mamíferos, por exemplo. E o conjunto dos mamíferos está contido dentro do conjunto animais.
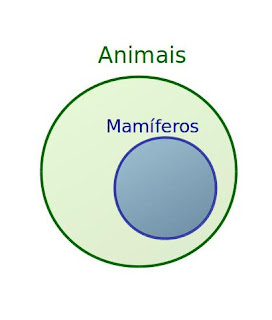 |
| Diagrama de Venn |
Podemos falar que o conjunto mamíferos está contido no conjunto animais. Ou que o conjunto animais contém o conjunto mamíferos.
A relação de inclusão é estabelecida somente entre conjuntos. No entanto, a relação de pertinência é estabelecida entre conjuntos e elementos.
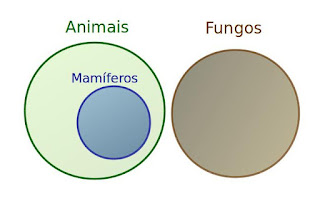 |
| Diagrama de Venn Relação de Inclusão |
O conjunto mamíferos está contido no conjunto animais.
$$\text{Mamíferos} \subset \text{Animais}$$
O conjunto animais contém o conjunto mamíferos.
$$\text{Animais} \supset \text{Mamíferos}$$
Da mesma maneira, podemos afirmar que um conjunto não contém um outro conjunto.
O conjunto fungos não está contido no conjunto mamíferos.
$$\text{Fungos} \not\subset \text{Mamíferos}$$
O conjunto mamíferos não contém o conjunto fungos.
$$\text{Mamíferos} \not\supset \text{Fungos}$$
Exemplo Matemático
Seja o conjunto A dos elementos x tal que x é número natural ímpar menor que 5.$$A = \{1, 3\}$$
E seja o conjunto B dos elementos x tal que x é número natural ímpar menor que 10.
$$B = \{1, 3, 5, 7, 9\}$$
Podemos dizer que $$A \subset B \Leftrightarrow \{\forall x \in A \Rightarrow x \in B\}$$.
 |
| Conjunto A contido em B |
Simbologia: o símbolo "⇔" significa equivalência e o símbolo "⇒" significa implica.
Entendendo os Subconjuntos
Um subconjunto, nada mais é do que um conjunto formado a partir de um conjunto original. Podemos criar o conjunto $$C = \{q, u, a, d, r, o\}$$ e, a partir dele, criarmos um subconjunto $$D = \{r, o, d, a\}$$. Podemos fazer as seguintes afirmações:
| Proposição | Equivalência | Valor |
|---|---|---|
| $$D$$ $$\subset$$ $$C$$ | $$\{r, o, d, a\}$$ $$\subset$$ $$\{q, u, a, d, r, o\}$$ | Verdadeiro |
| $$C$$ $$\supset$$ $$D$$ | $$\{q, u, a, d, r, o\}$$ $$\supset$$ $$\{r, o, d, a\}$$ | Verdadeiro |
| $$D$$ $$\not\subset$$ $$C$$ | $$\{r, o, d, a\}$$ $$\not\subset$$ $$\{q, u, a, d, r, o\}$$ | Falso |
| $$C$$ $$\not\supset$$ $$D$$ | $$\{q, u, a, d, r, o\}$$ $$\not\supset$$ $$\{r, o, d, a\}$$ | Falso |
| $$C$$ $$\not\subset$$ $$D$$ | $$\{q, u, a, d, r, o\}$$ $$\not\subset$$ $$\{r, o, d, a\}$$ | Verdadeiro |
| $$D$$ $$\not\supset$$ $$C$$ | $$\{r, o, d, a\}$$ $$\not\supset$$ $$\{q, u, a, d, r, o\}$$ | Verdadeiro |
| $$D$$ $$\supset$$ $$C$$ | $$\{r, o, d, a\}$$ $$\supset$$ $$\{q, u, a, d, r, o\}$$ | Falso |
| $$C$$ $$\subset$$ $$D$$ | $$\{q, u, a, d, r, o\}$$ $$\subset$$ $$\{r, o, d, a\}$$ | Falso |
Neste exemplos vimo o caso de $$D = \{r, o, d, a\}$$ em que r, o, d e a são elementos do conjunto $$D$$. E $$D$$ é subconjunto do conjunto $$C$$.
O Conjunto Vazio
Todo conjunto vazio é subconjunto de qualquer conjunto, inclusive de si mesmo.$$\forall A \Rightarrow \varnothing \subset A$$
Para qualquer que seja o conjunto A, o conjunto vazio está contido nele. Mas tome cuidado e preste atenção nos seguintes casos:
$$\varnothing \in \{1, 2, 3\}$$
Afirmação falsa. Pois o conjunto vazio estar contido em todos os conjuntos não implica que ele seja elemento de todos os conjuntos.
$$\varnothing \in \{\varnothing, 1, 2, 3\}$$
Afirmação verdadeira. Nesse conjunto, o conjunto vazio é elemento.
$$\varnothing \subset \{1, 2, 3\}$$
Afirmação verdadeira. O conjunto vazio é subconjunto de qualquer conjunto, como já vimos.
$$\varnothing \subset \{\varnothing, 1, 2, 3\}$$
Afirmação verdadeira também. Embora há o conjunto vazio como elemento, o conjunto vazio é subconjunto de qualquer conjunto.
Por que o Conjunto Vazio é Subconjunto de Qualquer Conjunto?
Para provar a afirmação de que o conjunto vazio é subconjunto de qualquer conjunto, seria preciso pegar todas as ocorrências de inclusão e garanti-las que são verdadeiras. Mas para negar matematicamente algo, basta que uma ocorrência que seja falsa. Portanto, escolheremos o segundo caminho, que é mais simples (também conhecido como prova por contradição ou redução ao absurdo).
Partindo desse pensamento, suponha o Conjunto $$A = \{1, 2, 3, 5, 8\}$$, e o conjunto vazio $$ = \{ \}$$.
- Suposição 1: o conjunto vazio não está contido em A, logo, todos os elementos do $$\varnothing$$ são diferentes dos elementos de $$A$$ (são disjuntos) e a interseção resulta em um conjunto vazio. Isso é uma contradição, e um absurdo, porque indica que o resultado da interseção ($$A \cap \varnothing = \varnothing$$) é em comum a ambos os conjuntos, e um deles é o próprio vazio. Ou, isso é uma contradição porque não há como dizer que todos os elementos do vazio são diferentes dos elementos de $$A$$, já que o vazio não contém elementos.
- Suposição 2: o conjunto vazio não está contido em A, logo, existe ao menos um ou alguns elementos diferentes dos elementos de $$A$$. Isso é uma contradição porque o vazio não possui elementos.
Conclusão: o vazio é subconjunto de qualquer conjunto, inclusive de si mesmo.
Todo Conjunto é Subconjunto Si Mesmo
Todo conjunto está contido em si mesmo. Matematicamente, pode ser representado dessa forma:
$$\forall A \Rightarrow A \subset A$$O símbolo $$\forall$$ significa "para qualquer que seja" ou "para todos".
O Conjunto das Partes de um Conjunto
Supondo o conjunto $$A = \{1, 2, 3\}$$, o conjunto $$P(A)$$ (lê-se: P de A) possui os seguintes elementos que são subconjuntos de $$A$$:
- o conjunto vazio;
- os conjuntos unitários {1},{2} e {3};
- os conjuntos com dois elementos {1, 2}, {1, 3} e {2, 3};
- o conjunto com três elementos (ele próprio) {1, 2, 3}.
$$P(A) = \{\varnothing$$, $$\{1\}$$, $$\{2\}$$, $$\{3\}$$, $$\{1,2\}$$, $$\{1,3\}$$, $$\{2,3\}$$, $$\{1,2,3\}\}$$
Pode ser representado em uma potência de base 2, sendo $$P(A) = 2^{3}$$ elementos, segundo o número de subconjuntos contidos em $$A$$. Se o conjunto B tem x elementos, então $$P(B) = 2^{x}$$.
Cuidado: O conjunto vazio e os outros conjuntos, como o conjunto $$\{1, 2\}$$ por exemplo, são elementos do conjunto $$P(A)$$. É correto afirmar que $$\{1,2\} \in P(A)$$ mas é incorreto afirmar que $$\{1,2\} \subset P(A)$$. Pois estamos falando dos elementos de $$P(A)$$ e não dos subconjuntos de $$A$$.
Note que:
$$\forall x \in P(A) \Rightarrow x \subset A$$
Outro Exemplo:
$$C = \{x ,y\}$$
$$P(C)$$ $$=$$ $$\{\varnothing, \{x\}, \{y\}, \{x, y\}\}$$ ou $$P(C)$$ $$=$$ $$\{\varnothing, \{x\}, \{y\}, C\}$$
Como $$C$$ possui dois elementos, $$P(C)$$ possui $$2^{2}$$ elementos, que são subconjuntos de $$C$$.
No próximo artigo veremos as operações que podem ser realizadas com conjuntos.
Considerações Finais
Neste artigo você aprendeu a relação estabelecida entre conjuntos e seus elementos, e que o elemento de um conjunto pode ser outro conjunto. Especificamente, você aprendeu:
- O que é um subconjunto.
- Relação de inclusão.
- O porquê do conjunto vazio ser subconjunto de qualquer conjunto.
- Que todo conjunto é subconjunto de si mesmo.
- O conjunto das partes de um conjunto.
Artigos
- Teoria dos Conjuntos - Introdução
- Teoria dos Conjuntos - Subconjuntos
- Teoria dos Conjuntos - Operações com Conjuntos (1/2)
- Teoria dos Conjuntos - Operações com Conjuntos (2/2)
- Teoria dos Conjuntos - Diferença Simétrica
- Teoria dos Conjuntos - Lei de De Morgan
- Exercícios
- Lista completa de artigos sobre teoria dos conjuntos
Referência Bibliográfica
BIANCHINI, E.; PACCOLA, H. Matemática. 2. ed. São Paulo: Moderna, 1997. 443 p.
BUCCHI, P. Curso Prático de Matemática 1. ed. São Paulo: Moderna, 1998. 578 p.
Para citar esse artigo:
 Pular para o conteúdo principal
Pular para o conteúdo principal
Comentários
Postar um comentário