Neste artigo será investigado as famosas notações científicas: sua origem, definição, uso, operações e exercícios propostos.
Notação Científica: Definição, Uso & Exercícios
O que é?
A notação científica é um sistema de notação que tem a utilidade de representar números que são muito grandes, ou, muito pequenos.
É dito que Arquimedes de Siracusa (287 – 212 A.E.C.) — um matemático e filósofo grego — foi talvez o primeiro estudioso a conceitualmente pensar e usar a notação. Arquimedes estava motivado a resolver um problema teórico complexo, o filósofo queria determinar quantos grãos de areia caberiam no universo, problema que foi trabalhado em sua obra conhecida como The Sand Reckoner ("O Contador de Areia"). Pela natureza do problema por si só, devido aos grãos de areia serem muito pequenos e o universo ser imensamente gigantesco, um novo sistema de notação numérica era necessário e assim surgiu primitivamente a primeira noção e estrutura similar a notação científica — que foi aprimorada séculos mais tarde até chegar em sua forma na qual é definida hoje.
Definição
Em outras palavras, por padrão, a mantissa deve ser um valor entre 1 e 10 incluindo o próprio 1, mas não igual a 10. Isso também significa que a mantissa não pode ser menor que 1 e nem maior que 10. Essa restrição garante que — independente de ser um número gigante, ou minúsculo — ele ainda possa ser escrito de forma simples com uma notação mais agradável e padronizada. Em seguida, esse número (a mantissa) se multiplica a constante 10 elevado a n, onde n é uma potência qualquer.
Com os seguintes exemplos abaixo e, em seguida, demonstrando as transformações, você entenderá melhor a definição. A definição se tornará mais natural para você.
Exemplos notáveis
|
| ESA & MPS for OSIRIS Team MPS/UPD/LAM/IAA/RSSD/INTA/UPM/DASP/IDA, via Wikimedia Commons |
$$ 6,39 \times 10^{23} \text{ kg} $$
Não seria muito prático escrever 639.000.000.000.000.000.000.000 por extenso toda vez que fosse necessário fazer referência ao valor da massa do planeta Marte. Com a notação científica, a escrita se torna simples e elegante.
Outro exemplo gigante: Arquimedes em sua obra O Contador de Areia estimou que a quantidade de grãos de areia para o preenchimento do universo seria um valor de 64 dígitos — que por motivos de comprimento, não será escrito por extenso aqui.
No entanto, como dito anteriormente, a notação científica serve não somente para números grandes, mas também para números pequenos. Vejamos mais um exemplo:
|
| Wikimedia, "Proton.svg". Domínio Publico. |
Como pode ser observado, há um detalhe diferente neste exemplo comparado com os outros: sua potência é negativa. Isso se deve ao fato de que a massa de um próton possui um valor muito pequeno, cerca de 0,000 000 000 000 000 000 000 000 001 672 6 kg. Note que — assim como evidenciado nos outros exemplos — também não é muito prático escrever por extenso números de valores muito pequenos.
Transformações
Apesar das transformações estarem classificadas em diferentes categorias abaixo, é meramente para fins de organização, não há diferença no método para os diferentes valores.
O segredo das transformações — se é que há algum — esta em movimentar a vírgula, para um dos lados, para que seja obtido um valor que obedeça a definição, sem modificá-lo, mas sim reescrevendo de tal forma que seja possível obter o valor original por extenso novamente. Observe os exemplos de transformações:
Transformações de números inteiros
I) $$ 1000 $$
Podemos afirmar que:
$$ 1000 = 1000,0 $$
Como 1000 é um valor maior que dez, é necessário reescrever o valor de tal forma que obedeça a definição. Sendo este um valor maior que dez, é preciso uma redução, para isso, será movimentado a vírgula para a esquerda até que seja achado um valor que se encaixe no intervalo da definição — ou seja, um valor entre um e dez.
$$ 1,000 $$
A vírgula foi movimentada 3 casas para a esquerda até se obter um valor dentro do intervalo da definição. Movimentar a vírgula para a esquerda, significa aumentar positivamente a potência n. Isso significa que a potência n terá o valor de 3 positivo, resultando em:
$$ 1 \times 10^3 $$
Note que, seu valor original continua lá, não foi modificado, está somente reescrito de outra forma — 10 vezes 10 vezes 10 é 1000 e 1000 vezes 1 é 1000. Logo:
$$ 1000 = 1 \times 10^3 $$
|
| Notação Científica exemplo 1. |
Transformações de números decimais
Novamente, o procedimento continua o mesmo, ou seja: movimentar a vírgula para a esquerda ou direita de forma que seja encontrado um valor da mantissa que se encaixe no intervalo da definição e elevar a base 10 no numero de casas que se foi movimentado a vírgula, sendo este negativo se para a direita ou positivo se para a esquerda.
II) $$ 3141,59 $$
$$ = 3,14159 \times 10^3 $$
III) $$ 0,0045 $$
Diferente dos outros exemplos anteriores, o exemplo III tem uma pequena diferença. Note que, o número tratado é menor que 1, isso significa que a vírgula terá que ser movida para a direita. E mover para a direita significa diminuir negativamente a potência n. Logo:
Movendo a vírgula três casas à direita obtemos: $$ 0004,5 $$. Logo a mantissa será $$ 4,5 $$. Portanto, resultando em:
IV) $$ 0,000000013 $$
$$ = 1,3 \times 10^{-8} $$
Operações
Não somente a escrita de valores se torna mais simples com o uso do padrão, mas a seguir será demonstrado que as operações aritméticas também.
Multiplicação
Para se multiplicar duas notações científicas é necessário multiplicar os "números soltos" (as duas mantissas), manter a multiplicação com a base 10 e somar os expoentes. Vejamos exemplos:
I) $$ 4,1 \cdot 10^{7} \times 2,3 \cdot 10^{3} $$
$$ = (4,1 \cdot 2,3) \times 10^{(7 + 3)} $$
$$ = 9,43 \times 10^{10} $$
Divisão
Para se dividir duas notações científicas o princípio continua o mesmo, exceto que onde você multiplicava, agora você divide e onde você somava, agora você subtrai. Ou seja, divida as duas mantissas, mantenha a multiplicação com a base 10 e subtraia os expoentes. Vejamos exemplos:
I) $$ 9,0 \cdot 10^{5} \div 2,0 \cdot 10^{3} $$
$$ = (9,0 \div 2,0) \times 10^{(5 - 3)} $$
$$ = 4,5 \times 10^{2} $$
II) $$ 8,8 \cdot 10^{-2} \div 4,0 \cdot 10^{1} $$
$$ = (8,8 \div 4,0) \times 10^{(-2 - 1)} $$
$$ = 2,2 \times 10^{-3} $$
III) $$ 4,1 \cdot 10^{-1} \div 2,0 \cdot 10^{-5} $$
$$ = (4,1 \div 2,0) \times 10^{(-1 - (-5))} $$
$$ = 2,05 \times 10^{4} $$
Adição e Subtração
Para efetuar a adição ou a subtração com notações científicas deve-se somar ou subtrair as duas mantissas e repetir a potência de 10. No entanto, para fazer essas operações, é necessário que as potências de 10 apresentem o mesmo expoente, devido as propriedades matemáticas de potenciação. Exemplos:
I) $$ 2,9 \cdot 10^{8} + 4,8 \cdot 10^{8} $$
$$ = (2,9 + 4,8) \cdot 10^{8} $$
$$ = 7,7 \times 10^{8} $$
III) $$ 7,54 \cdot 10^{2} + 1,113 \cdot 10^{2} $$
$$ = (7,54 + 1,113) \cdot 10^{2} $$
$$ = 8,653 \times 10^{2} $$
Exercícios
I) Represente o número $$ 1.776 $$ em notação científica.
II) Represente o número $$ 0,41 $$ em notação científica.
III) $$ 1,2 \cdot 10^{3} \times 2,0 \cdot 10^{1} $$
IV) $$ 9,0 \cdot 10^{6} \div 3,0 \cdot 10^{-5} $$
V) $$ 3,0 \cdot 10^{6} + 4,0 \cdot 10^{6} $$
VI DESAFIO) $$ 9 \cdot 10^{-16} \times 4,7 \cdot 10^{-24} \times 8,2 \cdot 10^{45} $$
I) $$ 1.776 $$
$$ = 1,776 \cdot 10^{3} $$
II) $$ 0,41 $$
$$ = 4,1 \cdot 10^{-1} $$
III) $$ 1,2 \cdot 10^{3} \times 2,0 \cdot 10^{1} $$
$$ = (1,2 \times 2,0) \cdot 10^{3 + 1} $$
$$ = 2,4 \cdot 10^{4} $$
IV) $$ 9,0 \cdot 10^{6} \div 3,0 \cdot 10^{-5} $$
$$ = (9,0 \div 3,0) \cdot 10^{(6 - (-5))} $$
$$ = 3,0 \cdot 10^{11} $$
V) $$ 3,0 \cdot 10^{6} + 4,0 \cdot 10^{6} $$
$$ = (3,0 + 4,0) \cdot 10^{6} $$
$$ = 7,0 \cdot 10^{6} $$
VI) $$ 9 \cdot 10^{-16} \times 4,7 \cdot 10^{-24} \times 8,2 \cdot 10^{45} $$
$$ = (9 \times 4,7 \times 8,2) \cdot 10^{(-16 + (-24) + 45)} $$
$$ = 346,86 \cdot 10^5 $$
$$ = 3,4686 \cdot 10^{7} $$
Para citar esse artigo:
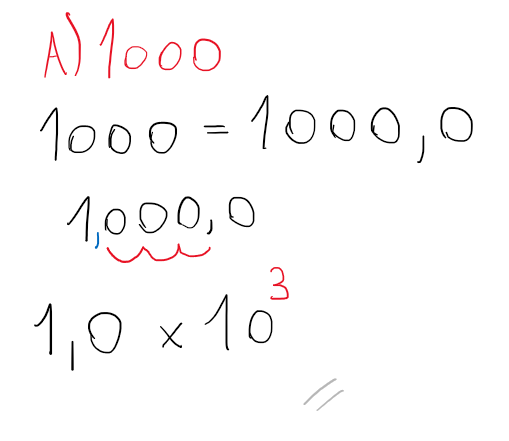
Gostei muito! me ajudou bastante com alguns exercícios escolares e aprendizado
ResponderExcluirPoxa, ficamos muito felizes com isso :)
Excluir